Начальные геометрические сведения Луч и угол  Сравнение и измерение углов Вертикальные и смежные углы Треугольник. Медианы, биссектрисы и высоты Первый признак равенства треугольников. Свойства равнобедренного треугольника Второй и третий признаки равенства треугольников Признаки параллельности прямых

 

"Сравнение и измерение отрезков".

 

После изучения этой темы:

Перед началом обучения обязательно распечатайте материал для работы (нажмите на изображение ниже):

 

 

Обратите внимание!

 

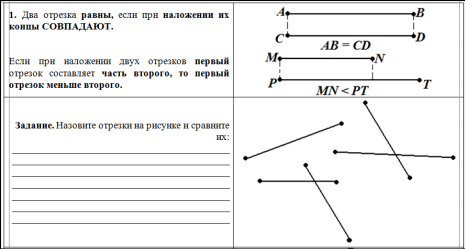
В левом столбце печатного материала находятся:

  • теоретические материалы;

  • формулировки заданий и место для записи ответа на задания.

В правом столбце печатного материала находятся:

  • графические иллюстрации к теоретическому материалу;

  • заготовки рисунков для выполнения задания;

  • или место для выполнения рисунка, если это есть в задании.

На втором листе материала - два образца решения типичных задач по этой теме и две задачи для самостоятельного решения.

Решение каждого примера подробно разобрано ниже. Внимательно ознакомьтесь с предложенными инструкциями, сравнивая их с печатным материалом. Далее попробуйте непосредственно в печатном материале решить предложенные задачи. После этого решите самостоятельную работу, представленную в отдельном печатном материале.

Ссылка: решение первого примера.

Ссылка: решение второго примера.

Чтобы распечатать самостоятельную работу, нажмите на изображение ниже:

 
Печатный материал содержит две страницы, которые выглядят так:
 

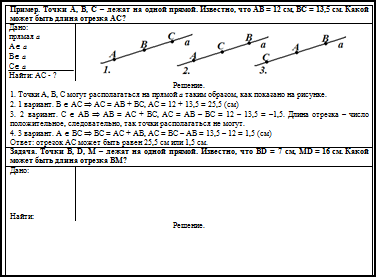
Пример 1. Точки А, В, С – лежат на одной прямой. Известно, что АВ = 12 см, ВС = 13,5 см. Какой может быть длина отрезка АС?

Общий вид решения задачи:

1. Любая геометрическая задача обязательно начинается с того, что записывается краткое условие - что дано в задаче. Условие пишем слева на странице с использованием обозначений и специальных символов. Сравните условие задачи и то, как записано краткое условие.

2. Справа от краткого условия обязательно располагается рисунок к задаче, составленный по условию задачи. Рисунок выполняется простым карандашом и по линейке.

В этой задаче не сказано, в каком порядке на прямой располагаются точки, поэтому здесь возможны три варианта расположения точек, что и отражено на рисунке к этой задаче.

3. Ниже "Дано" и рисунка к задаче посередине страницы пишем слово "Решение:".

[Каждый шаг в решении задачи обязательно нумеруется и обязательно должен содержать все необходимые теоретические пояснения. Например, первое действие в этой задаче разъясняет то, как составлен рисунок к этой задаче.]

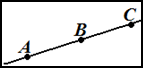
4. Во втором действии рассматривается 1 вариант расположения точек на прямой.

1 вариант (т. В лежит между точками А и С). Это в решении отмечено так: В Î АС. Следовательно (Þ),  можно записать равенство: АС = АВ + ВС. Затем подставим вместо АВ и ВС их значение: АС = АВ + ВС = 12 + 13,5 = 25,5 (см).

Обратите внимание: размерность ставится только после получения окончательного результата и обязательно в скобках.

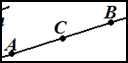
5. В третьем действии рассматривается 2 вариант расположения точек на прямой.

2 вариант (т. С лежит между точками А и В). Это в решении отмечено так: С Î АВ. Следовательно (Þ), можно записать такое равенство: АВ = АС + ВС. Подставим в это равенство значения для АВ и ВС, получим: 12 = АС + 13,5. Затем выразим АС: АС = АВ - ВС = 12 - 13,5; АС = -1,5 (см).

Обратите внимание: в данном случае длина отрезка получилась числом отрицательным, что невозможно по определению длины отрезка. Поэтому такой вариант расположения точек А, В и С невозможен.

6. В четвёртом действии рассматривается 3 вариант расположения точек на прямой.

3 вариант (т. А лежит между точками В и С). Это в решении отмечено так: А Î ВС. Следовательно (Þ), можно записать такое равенство: ВС = АС + АВ. Подставим в это равенство значения для АВ и ВС, получим: 13,5 = АС + 12, откуда выразим АС: АС = ВС - АВ = 13,5 - 12 = 1,5 (см).

7. После решения задачи обязательно записывается Ответ. Ответ в задаче - это развёрнутое предложение, содержащее ответ на поставленный в задаче вопрос. Поэтому размерность в Ответе не заключается в скобки!

 

Пример 2. Точка С – середина отрезка АВ, равного 64 см. На луче СА отмечена точка D так, что СD = 15 см. Найдите длины отрезков BD и AD.
Общий вид решения задачи:
Слева на странице запишем Дано.

Справа от Дано чертим рисунок. Так как С - середина АВ, то отрезки АС и СВ равны. Отметим это штрихами на рисунке.  

Под условием и рисунком напишем слово "Решение:".
В первом действии используем условие, что С - середина АВ. Из того, что С - середина АВ, следует (Þ), что АВ = АС + СВ и что АС = СВ = 1/2 АВ (по определению середины отрезка).:

  

Во втором действии объясняем, почему точка D принадлежит именно отрезку АС и находим длину отрезка AD. D лежит на луче СА, но может не принадлежать отрезку АС. Так как CD = 15 см (по условию), а отрезок АС = 32 см, то получается, что CD < AC, при этом точки А и D лежат по одну сторону от точки С (лежат на луче СА). Следовательно (Þ), D принадлежит отрезку АС:

   Тогда АС состоит из отрезков AD  и DC (AC = AD + DC). Выразим AD: AD = AC - DC, и подставим значения АС и DC: AD = AC - DC = 32 - 15 = 17 (см). Как всегда в решении размерность ставим в скобках после получения числового значения величины.

В третьем действии находим длину отрезка BD.  Если D принадлежит АС, то D принадлежит и отрезку АВ (D Î AB). Отсюда следует (Þ), что отрезок АВ состоит из AD и BD (АВ = AD + BD). Выразим BD из полученного равенства и подставим значения АВ и AD: BD = AB - AD = 64 - 17 = 47 (см).

Не забудем написать развёрнутый Ответ на поставленный в задаче вопрос:

 

ВЕРНУТЬСЯ НАВЕРХ ВЕРНУТЬСЯ К ПРИМЕРУ 1 ПЕЧАТЬ МАТЕРИАЛА ПЕЧАТЬ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

©Материал подготовлен учителем математики Максимовской Мариной Алексеевной