6

Начальные геометрические сведения Луч и угол Сравнение и измерение отрезков Сравнение и измерение углов Вертикальные и смежные углы Первый признак равенства треугольников. Свойства равнобедренного треугольника Второй и третий признаки равенства треугольников Признаки параллельности прямых

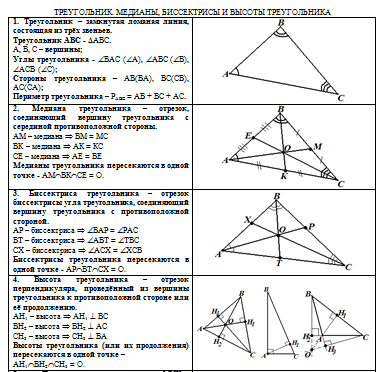
"Треугольник. Медианы, биссектрисы и высоты треугольника".

После изучения этой темы:

Вы вспомните, что такое геометрическая фигура, которая называется "треугольник", обозначение треугольника и его основных элементов;
Узнаете, что такое медиана, биссектриса и высота треугольника, их основные свойства;
Научитесь строить медиану, биссектрису и высоту треугольника.

Перед началом обучения обязательно распечатайте материал для работы (нажмите на изображение ниже):

Обратите внимание! В левом столбце печатного материала находятся: теоретические материалы; формулировки заданий и место для записи ответа на задания. В правом столбце печатного материала находятся: графические иллюстрации к теоретическому материалу; заготовки рисунков для выполнения задания; или место для выполнения рисунка, если это есть в задании. Кроме теории материал содержит три задачи на построение, для которых уже выполнены заготовки рисунков. Слева от заготовки необходимо записать Построение (последовательность действий) с помощью условных обозначений. Ниже представлены примеры построения медианы, биссектрисы и высоты треугольника.
Печатный материал содержит две страницы, которые выглядят так:

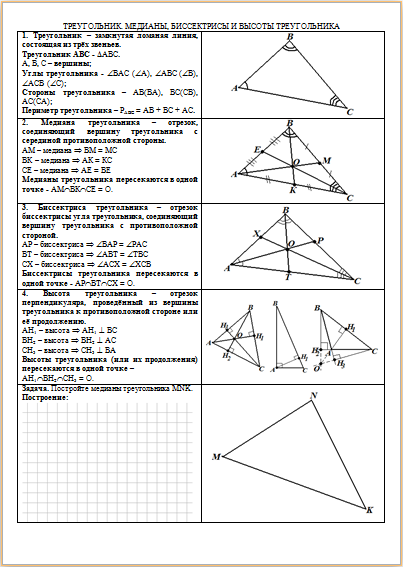
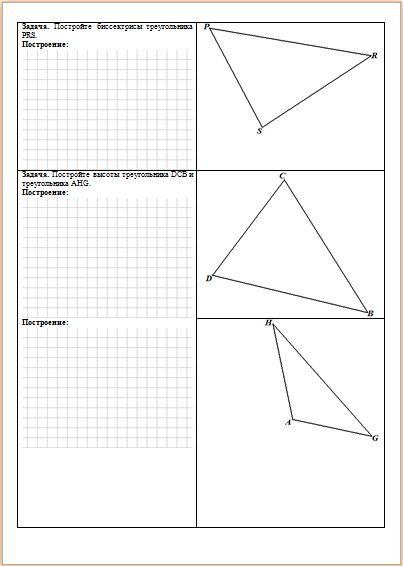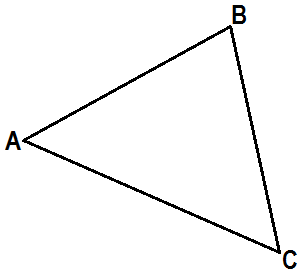
Пример 1. Построение медианы треугольника. Необходимы инструменты: линейка, карандаш, циркуль.

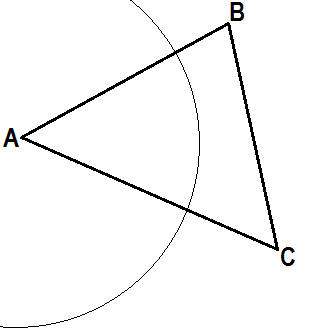
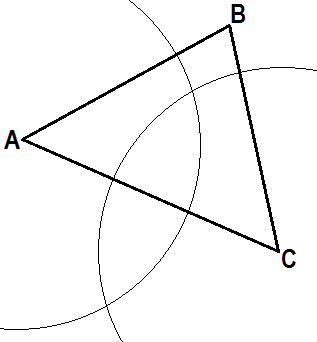
Дан треугольник АВС.	Строим окружность с центром в т. А и произвольным радиусом r (r < AC). [Окр. (А; r)]	Строим окружность с центром в т. C и тем же произвольным радиусом r. [Окр. (C; r)]

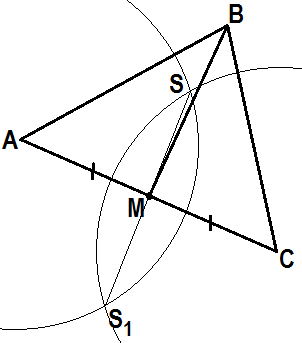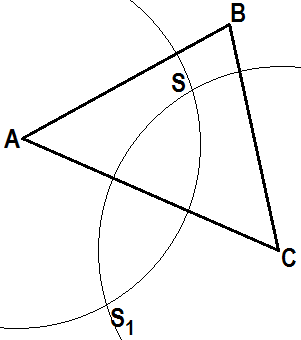
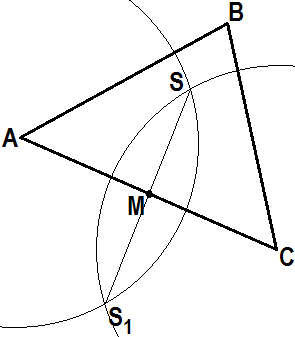
Эти окружности пересекаются в двух точках S и S₁. [Окр. (А; r)ÇОкр. (C; r) = S, S₁]	Отрезок SS₁ пересекает отрезок АС в т. М - его середине. [SS₁ÇАС = M]	Строим ВМ - биссектрису треугольника АВС.
Общий вид решения задачи:

Пример 2. Построение биссектрисы треугольника. Необходимы инструменты: линейка, карандаш, циркуль.

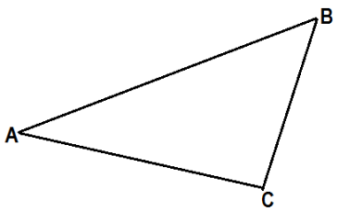
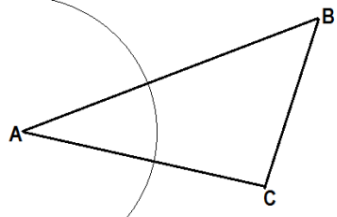
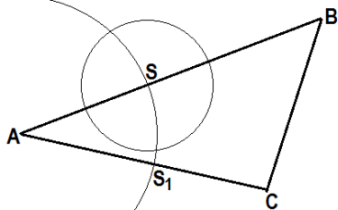
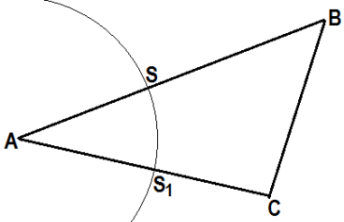
Дан треугольник АВС.	Строим окружность с центром в т. А и произвольным радиусом r. [Окр. (А; r)]	Окружность с центром в т. А и произвольным радиусом r пересекает стороны треугольника в точках S и S₁. [Окр. (А; r)ÇАВ = S, Окр. (А; r)ÇАC = S₁]

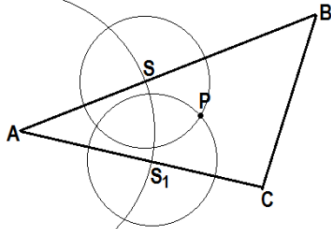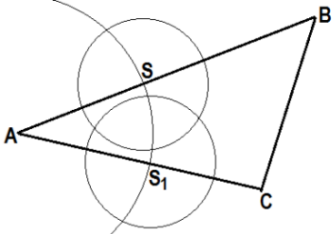
Строим окружность с центром в т. S и произвольным радиусом r₁. [Окр. (S; r₁)].	Строим окружность с центром в т. S₁ и произвольным радиусом r₁. [Окр. (S₁; r₁)].	Эти окружности пересекаются в точке Р. [Окр. (S; r₁) Ç Окр. (S₁; r₁) = P].
	Общий вид решения задачи:
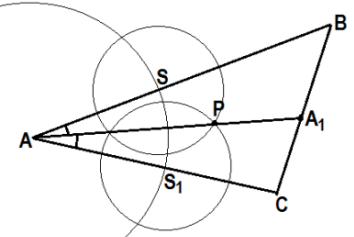
Луч АР - биссектриса угла ВАС, пересекает сторону ВС в точке А₁, следовательно, АА₁ - биссектриса треугольника АВС.	Общий вид решения задачи:
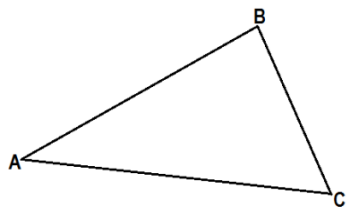
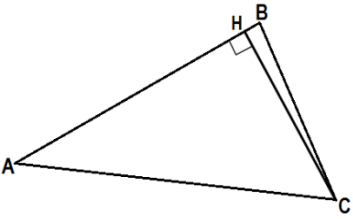
Пример 3. Построение высоты треугольника. Необходимые инструменты: линейка, угольник, карандаш.

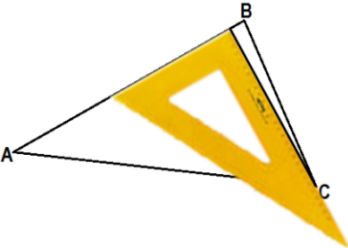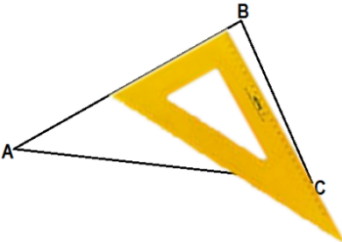
Дан треугольник АВС.	Приложим угольник так, как показано на рисунке (один катет угольника расположен на стороне АВ, второй катет угольника проходит через вершину С)	Из вершины С проведём отрезок вдоль катета угольника до стороны АВ.

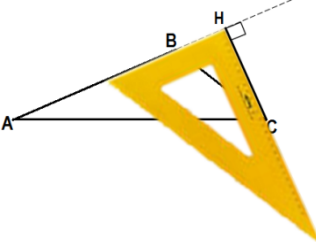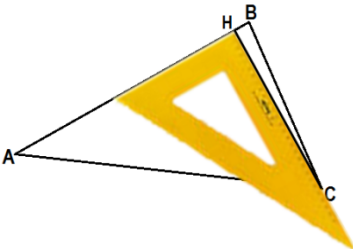
Обозначим получившуюся точку - Н. Угол АНС - прямой.	Т.к. точка Н лежит на стороне АВ и угол АНС - прямой, то СН - высота треугольника АВС.	Если треугольник тупоугольный (например, угол В - тупой), то для построения высоты угольник надо приложить к продолжению стороны АВ (как показано на рисунке)
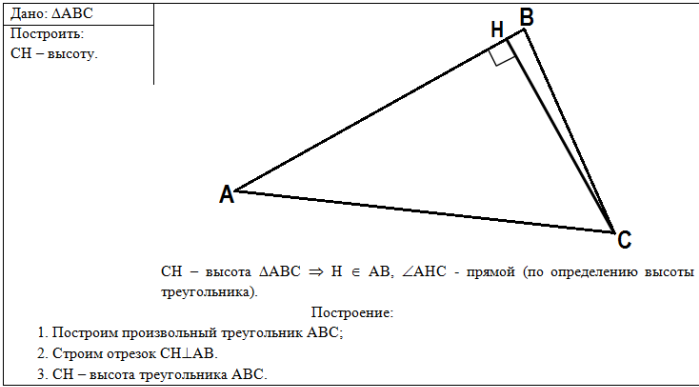
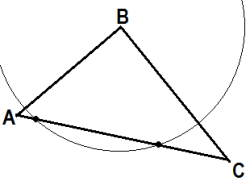
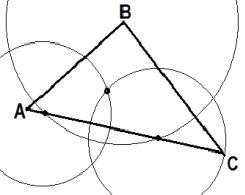
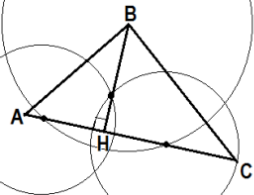
Общий вид решения задачи:		*Построение высоты с помощью карандаша, линейки и циркуля (дополнительно)**

ВЕРНУТЬСЯ НАВЕРХ К ПОСТРОЕНИЮ МЕДИАНЫ К ПОСТРОЕНИЮ БИССЕКТРИСЫ К ПОСТРОЕНИЮ ВЫСОТЫ ПЕЧАТЬ МАТЕРИАЛА