![]() Начальные геометрические сведения
Начальные геометрические сведения
![]() Луч и угол
Луч и угол
![]() Сравнение
и измерение отрезков
Сравнение
и измерение отрезков
![]() Сравнение
и измерение углов
Сравнение
и измерение углов
![]() Треугольник.
Медианы, биссектрисы и высоты
Треугольник.
Медианы, биссектрисы и высоты
![]() Первый
признак равенства треугольников. Свойства равнобедренного треугольника
Первый
признак равенства треугольников. Свойства равнобедренного треугольника
![]() Второй
и третий признаки равенства треугольников
Второй
и третий признаки равенства треугольников
![]() Признаки
параллельности прямых
Признаки
параллельности прямых
"Вертикальные и смежные углы".
После изучения этой темы:
Вы познакомитесь с двумя новыми понятиями - "вертикальные углы", "смежные углы";
Узнаете их основные свойства;
Научитесь решать задачи по этой теме.
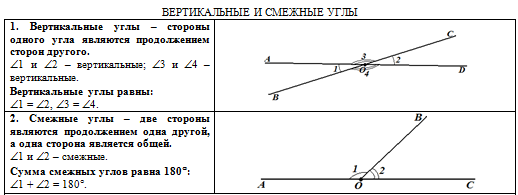
Перед началом обучения обязательно распечатайте материал для работы (нажмите на изображение ниже):
|
Обратите внимание!
В левом столбце печатного материала находятся:
В правом столбце печатного материала находятся:
|
 |
|
|
Материал содержит решение трёх типичных задач по этой теме и задачи для самостоятельного решения. Решение примеров подробно разобрано ниже. Внимательно ознакомьтесь с предложенными инструкциями, сравнивая их с печатным материалом. Далее попробуйте непосредственно в печатном материале решить предложенные задачи. Ссылки: решение Задачи 1, решение Задачи 2, решение Задачи 3. |
||
| Печатный материал содержит две страницы, которые выглядят так: | ||
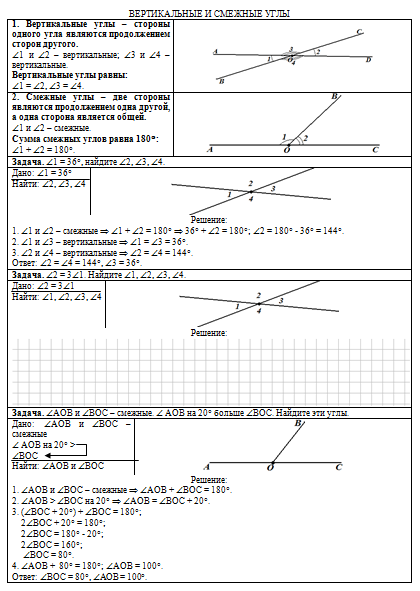
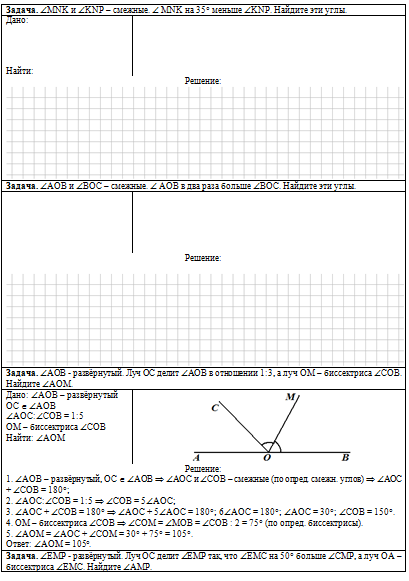 |
||
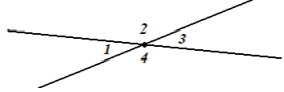
| Задача 1. Угол 1 равен 36º, найти углы 2, 3 и 4. |
Общий вид решения задачи:
|
|
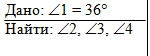 |
 |
|
| Слева запишем краткое условие задачи с помощью условных обозначений. | Справа выполним чертёж по данным задачи. В процессе решения на чертёже можно выполнять дополнительные построения или обозначать найденные элементы. | |
| Посередине листа запишем слово "Решение:" | ||
|
В первом действии рассмотрим углы 1 и 2. Так как эти углы смежные, то их сумма равна 180º (по свойству смежных углов). Отметим этот факт в решении:
Подставим вместо угла 1 его градусную меру:
|
||
|
Во втором действии рассмотрим углы 1 и 3. Так как эти углы вертикальные, то они равны (по свойству вертикальных углов). Отметим этот факт в решении:
|
||
|
В третьем действии рассмотрим углы 2 и 4. Так как эти углы вертикальные, то они равны (по свойству вертикальных углов). Отметим этот факт в решении:
|
||
|
После решения напишем Ответ:
|
||
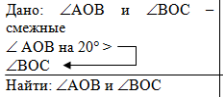
| Задача 2. Углы АОВ и ВОС смежные. Известно, что угол АОВ на 20º больше угла ВОС. Найти углы АОВ и ВОС. |
Общий вид решения задачи:
|
|
 |
 |
|
| Слева запишем краткое условие задачи, используя условные обозначения. | Справа выполним чертёж по данным задачи. В процессе решения на чертёже можно выполнять дополнительные построения или обозначать найденные элементы. | |
|
Под условием и рисунком посередине листа запишем слово "Решение:". |
||
|
В первом действии рассмотрим углы АОВ и ВОС. Так как они смежные, то их сумма равна 180º (по свойству смежных углов). Отметим это в решении:
|
||
|
Во втором действии используем условие, что угол АОВ на 20º больше угла ВОС, и выразим угол АОВ через угол ВОС:
|
||
|
В третьем действии в равенство ÐAOВ + ÐВОС = 180º подставим вместо угла АОВ полученное выше выражение ÐВOC + 20º:
|
||
|
|
|
|
|
В четвёртом действии снова используем равенство ÐAOВ + ÐВОС = 180º, подставим вместо угла ВОС полученное значение 80º и вычислим угол АОВ:
|
||
|
Далее запишем Ответ на поставленный в задаче вопрос:
|
||
| Задача 3. Луч ОС делит развёрнутый угол АОВ в отношении 1:5, а луч ОМ - биссектриса угла СОВ. Найти угол АОМ. |
Общий вид решения задачи:
|
|
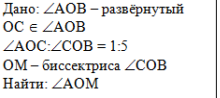 |
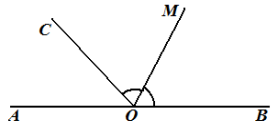 |
|
| Слева запишем краткое условие задачи, используя условные обозначения. | Справа выполним чертёж по данным задачи. В процессе решения на чертёже можно выполнять дополнительные построения или обозначать найденные элементы. | |
| Под условием и рисунком посередине листа запишем слово "Решение:". | ||
|
В первом действии воспользуемся условиями, что угол АОВ развёрнутый, а луч ОС лежит внутри этого угла, тогда углы АОС и СОВ - смежные (по определению смежных углов). Отметим это в решении:
следовательно, по свойству смежных углов:
|
||
|
Во втором действии используем условие, что луч ОС делит угол АОВ в отношении 1:5, т.е.:
Используем основное свойство пропорции (произведение средних членов равно произведению крайних) получим:
|
||
|
В третьем действии используем вывод, полученный в первом действии, что
и решим получившееся уравнение:
Подставим
полученное значение угла АОС в равенство
|
||
|
В четвёртом действии воспользуемся условием, что луч ОМ - биссектриса угла СОВ и определением биссектрисы:
|
||
|
В пятом действии воспользуемся условием, что угол АОМ состоит из углов АОС и СОМ (по рисунку к задаче):
|
||
|
Запишем Ответ на поставленный вопрос:
|
||
ВЕРНУТЬСЯ НАВЕРХ
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 1
ВЕРНУТЬСЯ К ЗАДАЧЕ 1
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 2
ВЕРНУТЬСЯ К ЗАДАЧЕ 2
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 3
ВЕРНУТЬСЯ К ЗАДАЧЕ 3
![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА
©Материал подготовлен учителем математики Максимовской Мариной Алексеевной