Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
Обратите внимание!
В левом
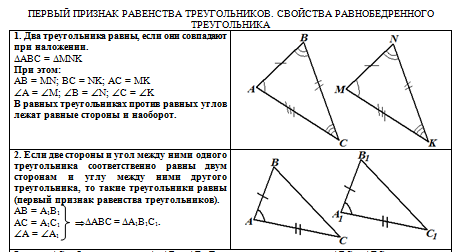
столбце печатного материала находятся:
В правом
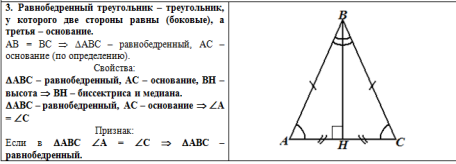
столбце печатного материала находятся:
-
графические иллюстрации к теоретическому материалу;
-
заготовки рисунков для выполнения задания;
-
или
место для выполнения рисунка, если это есть
в задании.
В материале
разобраны пять задач и ещё пять задач предложено решить прямо в
материале (для этого есть заготовки). Ниже приведены ссылки на
разобранные решения задач:
задача 1,
задача 2,
задача 3,
задача 4,
задача 5.
|
 |
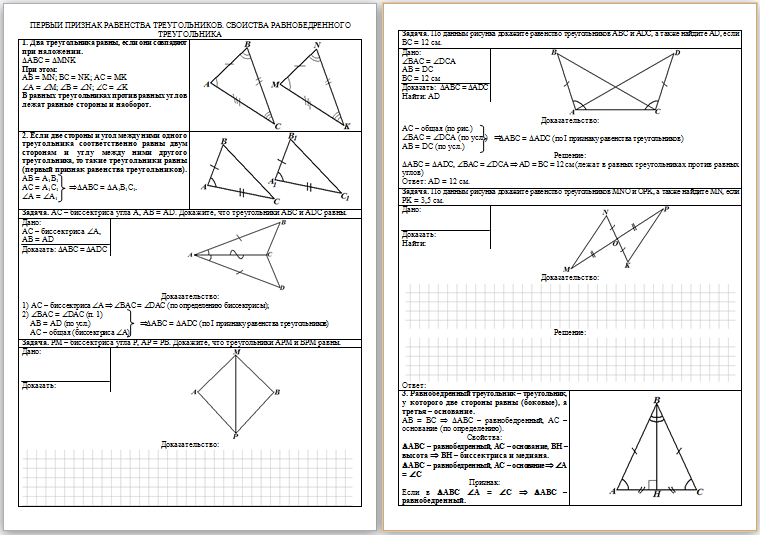
| Печатный
материал содержит четыре страницы, которые выглядят так: |
|
 |
|
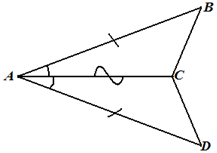
Задача 1.
АС - биссектриса угла А. АВ = AD.
Докажите, что треугольники АВС и ADС равны. |
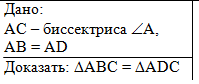 |
 |
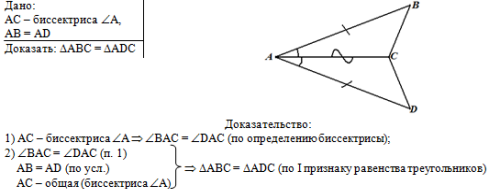
Общий вид решения задачи:
|
|
Слева запишем краткое условие задачи с помощью условных обозначений |
Справа выполним рисунок по условию задачи. Рисунок можно дополнить
(например, отметить общую сторону АС) |
|
Посередине под условием и рисунком напишем слово "Доказательство:" |
|
В первом действии
используем условие, что АС - биссектриса угла А и воспользуемся
определением биссектрисы, сделаем вывод, что углы ВАС и
DAC равны:
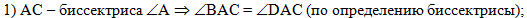 |
|
Во втором действии
объединим три условия, необходимые для использования первого признака
равенства треугольников (необходимо соответственное равенство двух
сторон и угла между ними у обоих треугольников):
 , ,
после чего сделаем вывод о
равенстве треугольников ВАС и DAC по первому
признаку равенства треугольников. Обязательно отметим это в
доказательстве:
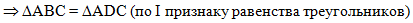 . . |
|
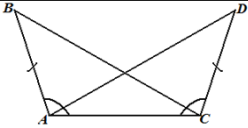
Задача 2. По
данным рисунка докажите равенство треугольников АВС и
ADC, а также найдите AD, если ВС = 12
см. |
 |
 |
Общий вид решения задачи:
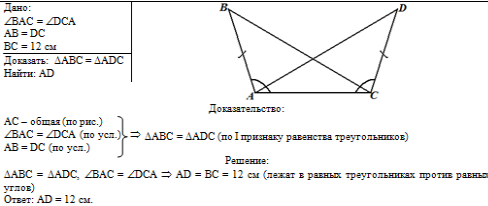
|
|
Слева запишем краткое условие к задаче. В данном случае необходимо
Доказать факт и Найти элемент треугольника. |
Справа начертим рисунок по условию задачи. В процессе доказательства и
решения рисунок можно дополнять. |
|
После условия и рисунка напишем слово "Доказательство:" |
|
Для доказательства соберём
все условия в задаче, необходимые для использования первого
признака равенства треугольников:
 . .
Этих условий достаточно,
чтобы сделать вывод, что треугольники АВС и ADC
равны по первому признаку равенства треугольников. Обязательно
отметим это в доказательстве:
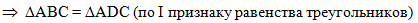 |
|
После завершённого доказательства напишем слово
"Решение:" |
|
|
В решении используем
доказанный факт равенства треугольников АВС и ADC
и условие, что углы ВАС и DCA равны:
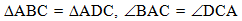 . .
Так как в равных
треугольниках против равных углов лежат равные стороны, то ВС =
AD. Обязательно отметим этот факт в решении:
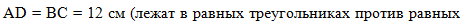 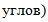 . . |
После решения запишем Ответ на поставленный вопрос:
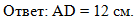 |
|
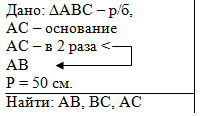
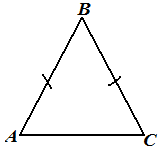
Задача 3. В
равнобедренном треугольнике основание в 2 раза меньше боковой стороны.
Найти стороны треугольника, если его периметр равен 50 см. |
 |
 |
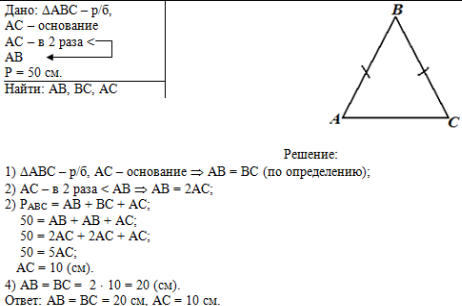
Общий вид решения
задачи:
|
|
Слева запишем краткое условие, используя условные обозначения. Т.к.
треугольник не назван, то выберем традиционное обозначение АВС и
определим, что АС - основание. |
Справа начертим рисунок по условию задачи |
|
После условия и рисунка напишем слово "Решение:". |
|
В первом действии
используем условие, что треугольник равнобедренный, АС - его основание:
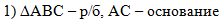 . .
Отсюда по определению
равнобедренного треугольника сделаем вывод, что две другие стороны (АВ
и ВС) равны:
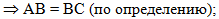 |
|
Во втором действии
используем условие, что АС в 2 раза меньше боковой стороны и выразим
боковую сторону АВ через основание АС:
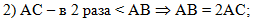 |
|
В третьем действии
используем факт, что периметр треугольника равен сумме длин
его сторон:
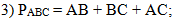
Так как периметр по условию
равен 50 см, а АВ = ВС (п. 1), то подставим в первое равенство вместо РАВС
- 50, а вместо ВС - АВ и запишем:
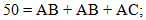
Если АВ = 2АС, то вместо АВ
подставим 2АС:
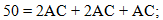 . .
После этого решим
получившееся уравнение:
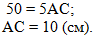 |
|
В четвёртом действии
найдём АВ = ВС из условия, что АВ = 2АС:
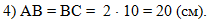 |
После решения напишем Ответ на поставленный вопрос:
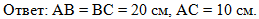 |
|
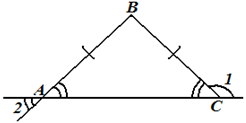
Задача 4. На
рисунке угол 1 равен 143º, а отрезок ВС равен
отрезку АВ. Найти угол 2. |
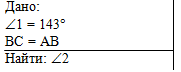 |
 |
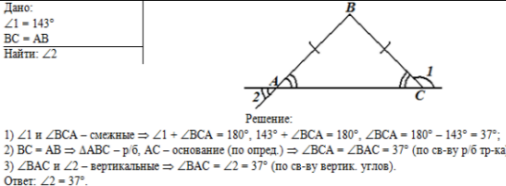
Общий вид решения задачи:
|
|
Слева по условию задачи напишем краткое условие. |
Справа начертим рисунок к задаче с необходимыми обозначениями. Рисунок
можно дополнить обозначениями очевидных фактов (например, равенства
вертикальных углов). |
|
После условия и рисунка напишем слово "Решение:" |
|
В первом действии
используем условие, отражённое на рисунке, что углы 1 и ВСА - смежные,
а, следовательно, их сумма равна 180º по свойству
смежных углов:
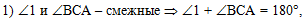
Подставим вместо угла 1 его
градусную меру (143º) и найдём угол ВСА:
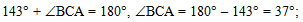 |
|
Во втором действии
используем условие, что ВС = АВ и по определению
равнобедренного треугольника сделаем вывод, что треугольник АВС -
равнобедренный, АС - его основание:
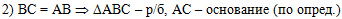 , ,
откуда сделаем вывод, что
углы ВСА и ВАС равны (по свойству углов при основании
равнобедренного треугольника):
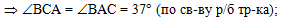 |
|
В третьем действии
используем условие, что углы ВАС и 2 - вертикальные, а,
следовательно, они равны:
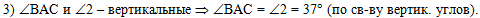 |
|
После решения запишем
Ответ на поставленный в задаче вопрос:
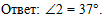 |
|
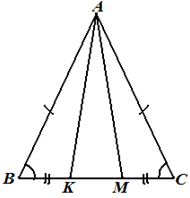
Задача 5. В
равнобедренном треугольнике АВС на основании ВС отметили точки К и М
так, что ВК = СМ. Докажите, что треугольники ВАК и САМ равны. Докажите,
что треугольник АКМ - равнобедренный. |
 |
 |
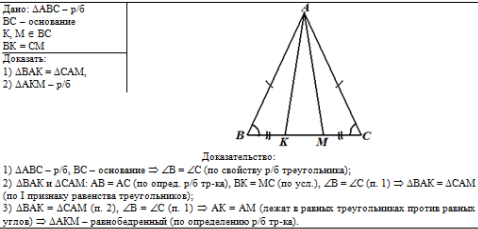
Общий вид решения задачи:
|
|
Слева по условию задачи запишем краткое условие с помощью условных
обозначений |
Справа от условия выполним чертёж по условиям задачи. Чертёж можно
дополнять обозначениями в процессе решения |
|
После условия и рисунка запишем слово "Доказательство:" |
|
В первом действии
используем условие, что треугольник АВС - равнобедренный с основанием
ВС. Откуда сделаем вывод, что углы В и С - равны по свойству
равнобедренного треугольника:
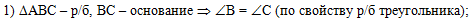 |
|
Во втором действии
рассмотрим треугольники ВАК и САМ -
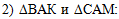
Перечислим всё, что нам про
них известно: АВ = АС (по определению, как боковые стороны
равнобедренного треугольника), ВК = МС (по условию задачи), углы В и С
равны (доказано в п. 1):
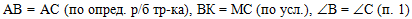 . .
Этих условий достаточно,
чтобы воспользоваться первым признаком равенства треугольников:
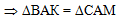 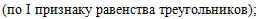
Доказан первый факт. |
|
В третьем действии
используем доказанное равенство треугольников ВАК и САМ (из п. 2) и
равенство углов В и С (из п. 1):
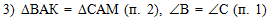 , ,
так как в равных
треугольниках против равных углов лежат равные стороны,
то АК = АМ:
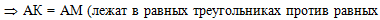 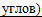 , ,
а если АК = АМ, то
треугольник АКМ - равнобедренный по определению равнобедренного
треугольника:
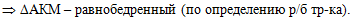
Доказан
второй факт. |
![]() Начальные геометрические сведения
Начальные геометрические сведения
![]() Луч и угол
Луч и угол
![]() Сравнение
и измерение отрезков
Сравнение
и измерение отрезков
![]() Сравнение
и измерение углов
Сравнение
и измерение углов
![]() Вертикальные
и смежные углы
Вертикальные
и смежные углы
![]() Треугольник.
Медианы, биссектрисы и высоты
Треугольник.
Медианы, биссектрисы и высоты
![]() Второй
и третий признаки равенства треугольников
Второй
и третий признаки равенства треугольников
![]() Признаки
параллельности прямых
Признаки
параллельности прямых ![]() К ЗАДАЧЕ 1
К ЗАДАЧЕ 1
![]() К ЗАДАЧЕ 2
К ЗАДАЧЕ 2
![]() К ЗАДАЧЕ 3
К ЗАДАЧЕ 3
![]() К ЗАДАЧЕ
4
К ЗАДАЧЕ
4
![]() К ЗАДАЧЕ
5
К ЗАДАЧЕ
5
![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА