Начальные геометрические сведения Луч и угол Сравнение и измерение отрезков  Вертикальные и смежные углы Треугольник. Медианы, биссектрисы и высоты Первый признак равенства треугольников. Свойства равнобедренного треугольника Второй и третий признаки равенства треугольников Признаки параллельности прямых

 

 "Сравнение и измерение углов".

 

После изучения этой темы:

Перед началом обучения обязательно распечатайте материал для работы (нажмите на изображение ниже):

 

 

Обратите внимание!

 

В левом столбце печатного материала находятся:

  • теоретические материалы;

  • формулировки заданий и место для записи ответа на задания.

В правом столбце печатного материала находятся:

  • графические иллюстрации к теоретическому материалу;

  • заготовки рисунков для выполнения задания;

  • или место для выполнения рисунка, если это есть в задании.

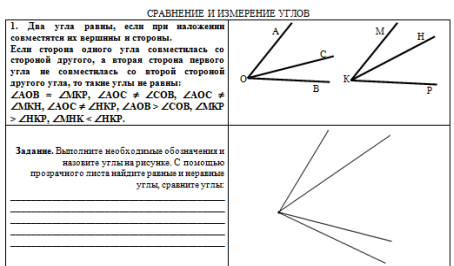На втором листе материала - образец решения типичной задачи по этой теме и задача для самостоятельного решения.

Решение примера подробно разобрано ниже. Внимательно ознакомьтесь с предложенными инструкциями, сравнивая их с печатным материалом. Далее попробуйте непосредственно в печатном материале решить предложенную задачу. После этого попробуйте решить самостоятельную работу, представленную в отдельном печатном материале.

Ссылка: решение примера.

Чтобы распечатать самостоятельную работу, нажмите на изображение ниже:
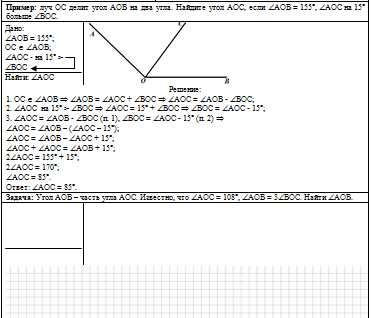Печатный материал содержит две страницы, которые выглядят так:

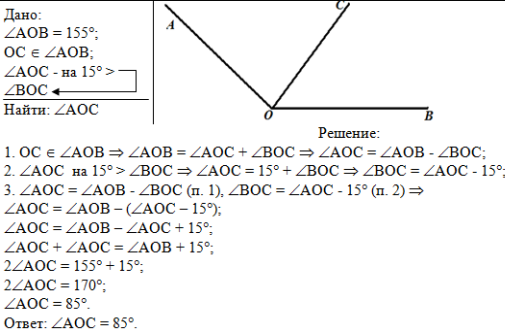
Пример: луч ОС делит угол АОВ на два угла. Найдите угол АОС, если ÐАОВ = 155°, ÐАОС на 15° больше ÐВОС.

 Общий вид решения задачи:
 
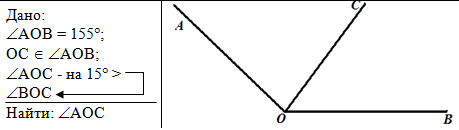Слева запишем краткое условие задачи с помощью условных обозначений Справа от краткого условия выполним чертёж по данным задачи. В процессе решения чертёж можно дополнять необходимыми элементами и условиями.  
Под условием и рисунком запишем слово "Решение":
В первом действии используем условие, что луч ОС принадлежит углу АОВ, тогда угол АОВ делится на два угла АОС и ВОС, откуда следует, что угол АОС - это разность углов АОВ и ВОС.
Во втором действии используем условие, что угол АОС на 15º больше угла ВОС. Тогда угол АОС равен углу ВОС плюс 15º, откуда следует, что угол ВОС - это разность угла АОС и 15º.
В третьем действии объединим выводы, полученные в первом и втором действиях:
подставим в разность, полученную в первом действии, вместо угла ВОС выражение ÐAOC - 15º.
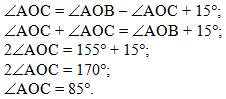Далее решим полученное уравнение.
Под решением запишем Ответ.

ВЕРНУТЬСЯ НАВЕРХ ВЕРНУТЬСЯ К ПРИМЕРУ ПЕЧАТЬ МАТЕРИАЛА ПЕЧАТЬ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

©Материал подготовлен учителем математики Максимовской Мариной Алексеевной