Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
Обратите внимание!
В левом
столбце печатного материала находятся:
В правом
столбце печатного материала находятся:
-
графические иллюстрации к теоретическому материалу;
-
заготовки рисунков для выполнения задания;
-
или
место для выполнения рисунка, если это есть
в задании.
Материал
содержит две разобранные задачи, четыре задачи предложено решить
самостоятельно.
Ссылки на
решение Задачи 1,
Задачи 2. |
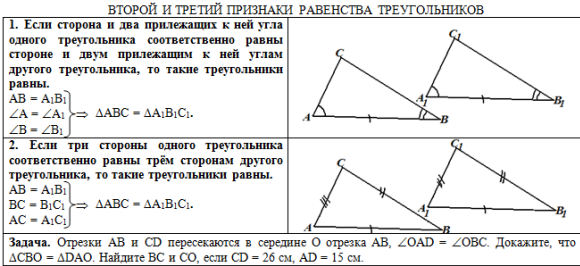 |
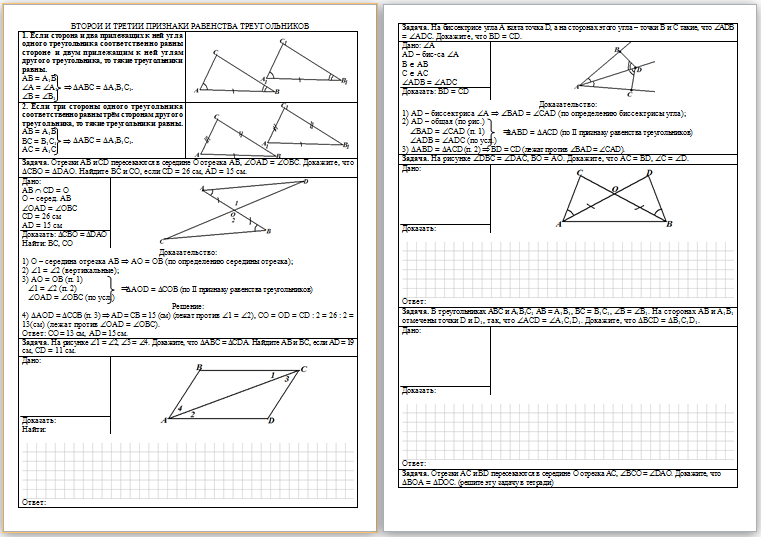
| Печатный
материал содержит две страницы, которые выглядят так: |
 |
|
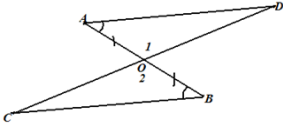
Задача 1. Отрезки АВ и
CD пересекаются в середине О отрезка АВ, углы
ОАВ и ОВС равны. Докажите, что треугольники СВО и DAO
равны. Найдите ВС и СО, если CD = 26 см,
AD = 15 см. |
 |
 |
Общий вид решения задачи:
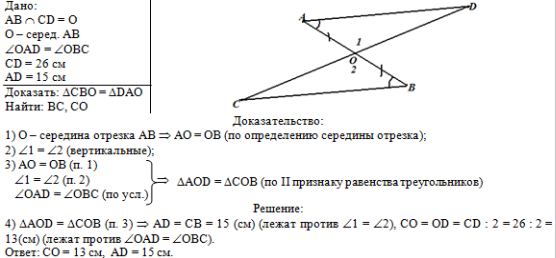
|
|
Слева запишем краткое условие задачи с помощью условных обозначений |
Справа от условия выполним чертёж по условию задачи. В процессе решения
этот чертёж можно дополнять обозначениями и элементами. |
|
Под условием и чертежом напишем слово "Доказательство:" |
|
В первом действии
используем условие, что О - середина отрезка АВ, а, следовательно, АО =
ОВ по определению середины отрезка:
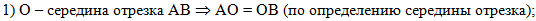 |
|
Во втором действии
отметим, что углы 1 и 2 равны, т.к. они вертикальные:
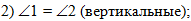 |
|
В третьем действии
соберём все условия, которые необходим для использования второго
признака равенства треугольников (должны быть соответственно равны
сторона и прилежащие к ней углы в каждом из треугольников):
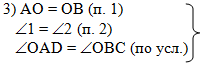 , ,
откуда сделаем вывод, что
треугольника AOD и СОВ равны по второму
признаку равенства треугольников:
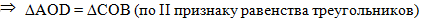 . .
Доказательство закончено. |
|
Под
доказательством запишем слово "Решение:" |
|
В четвёртом действии
используем только что доказанное равенство треугольников
AOD и СОВ:
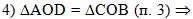
из равенства этих
треугольников следует равенство сторон AD и СВ
(т.к. они лежат в равных треугольниках против равных углов
1 и 2):
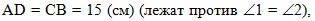
также СО =
OD, т.к. лежат против равных углов OAD
и OBC, тогда О - середина отрезка
CD, а если CD = 26
см, то по определению середины отрезка СО = OD
= CD : 2 = 13 см:
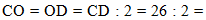 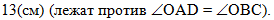 |
|
После решения запишем Ответ:
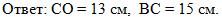 |
|
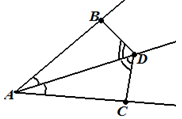
Задача 2. На биссектрисе угла А взята точка
D, а на сторонах угла взяты точки В и С так,
что углы ADB и ADC
равны. Докажите, что BD = DC. |
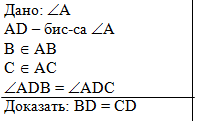 |
 |
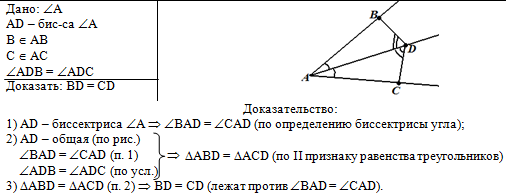
Общий вид решения задачи:
|
|
Слева запишем краткое условие задачи с помощью условных обозначений. |
Справа от условия задачи выполним чертёж по условию задачи, который в
процессе решения можно дополнять различными обозначениями и элементами. |
|
Под условием и чертежом напишем слово "Доказательство:" |
|
В первом действии
воспользуемся условием, что AD - биссектриса
угла А:
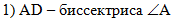 , ,
тогда по определению
биссектрисы угла углы BAD и
CAD равны:
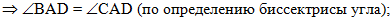 |
|
Во втором действии
объединим все условия, необходимые для использования второго признака
равенства треугольников:
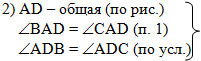 , ,
этих условий достаточно,
чтобы сделать вывод, что треугольники ABD и
ACD равны по второму признаку равенства треугольников:
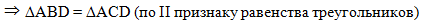 / / |
|
В третьем действии
используем только что доказанный факт равенства треугольников
ABD и ACD:
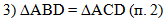
т.к. в равных треугольников
против равных углов BAD и
CAD лежат равные стороны BD и
CD:
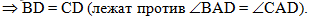 |
![]() Начальные геометрические сведения
Начальные геометрические сведения
![]() Луч и угол
Луч и угол
![]() Сравнение
и измерение отрезков
Сравнение
и измерение отрезков
![]() Сравнение
и измерение углов
Сравнение
и измерение углов
![]() Вертикальные
и смежные углы
Вертикальные
и смежные углы
![]() Треугольник.
Медианы, биссектрисы и высоты
Треугольник.
Медианы, биссектрисы и высоты
![]() Первый
признак равенства треугольников. Свойства равнобедренного треугольника
Первый
признак равенства треугольников. Свойства равнобедренного треугольника
![]() Признаки
параллельности прямых
Признаки
параллельности прямых ![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 1
ВЕРНУТЬСЯ К ЗАДАЧЕ 1
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 2
ВЕРНУТЬСЯ К ЗАДАЧЕ 2
![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА