Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
Обратите внимание!
В левом
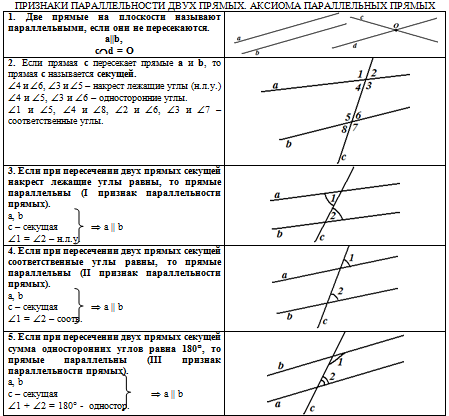
столбце печатного материала находятся:
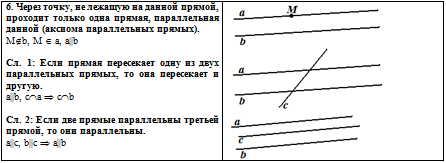
В правом
столбце печатного материала находятся:
-
графические иллюстрации к теоретическому материалу;
-
заготовки рисунков для выполнения задания;
-
или
место для выполнения рисунка, если это есть
в задании.
Материал
содержит одну разобранную задачу и четыре задачи предложено решить
самостоятельно.
Ссылка на
разобранное решение этой задачи. |
  |
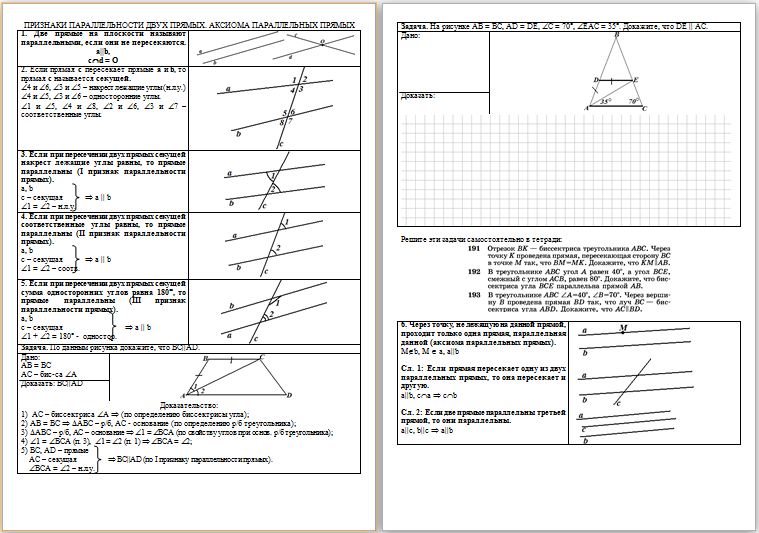
| Печатный
материал содержит две страницы, которые выглядят так: |
 |
|
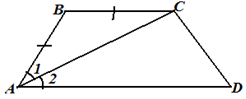
Задача. По данным рисунка докажите, что ВС параллельна
AD. |
|
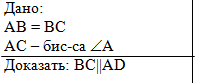 |
 |
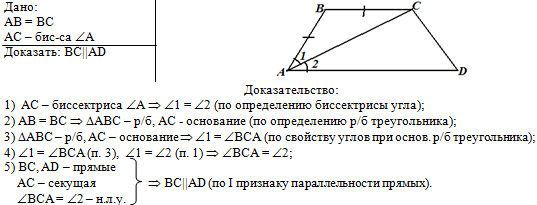
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Доказательство:" |
|
В первом действии
используем условие, что АС - биссектриса угла А:
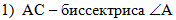 , ,
откуда по определению
биссектрисы угла сделаем вывод, что равны углы 1 и 2, обозначенные
на рисунке:
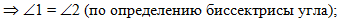 |
|
Во втором действии
используем условие, что АВ = ВС:
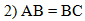 , ,
если эти отрезки равны, то
треугольник АВС - равнобедренный с основанием АС, по определению
равнобедренного треугольника:
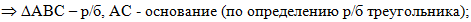 |
|
В третьем действии
используем только что доказанный факт, что треугольник АВС
равнобедренный и АС - его основание:
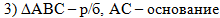 , ,
откуда по свойству углов
при основании равнобедренного треугольника получаем, что угол 1
равен углу ВСА:
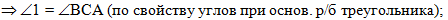 |
|
В четвёртом действии,
зная, что угол 1 равен как углу 2 (из п. 1), так и углу ВСА (из п. 3),
делаем вывод, что угол ВСА равен углу 2:
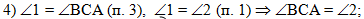 |
|
В пятом действии
объединяем все условия, которые необходимы для использования первого
признака параллельности прямых (необходимо, чтобы две прямые были
пересечены третье (секущей), и чтобы накрест лежащие углы в этом случае
были равны):
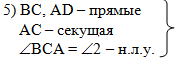 . .
Этого достаточно, чтобы
сделать вывод, что прямые ВС и AD параллельны:
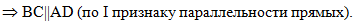 |
![]() Начальные геометрические сведения
Начальные геометрические сведения
![]() Луч и угол
Луч и угол
![]() Сравнение
и измерение отрезков
Сравнение
и измерение отрезков
![]() Сравнение
и измерение углов
Сравнение
и измерение углов
![]() Вертикальные
и смежные углы
Вертикальные
и смежные углы
![]() Треугольник.
Медианы, биссектрисы и высоты
Треугольник.
Медианы, биссектрисы и высоты
![]() Первый
признак равенства треугольников. Свойства равнобедренного треугольника
Первый
признак равенства треугольников. Свойства равнобедренного треугольника
![]() Второй
и третий признаки равенства треугольников
Второй
и третий признаки равенства треугольников
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ
ВЕРНУТЬСЯ К ЗАДАЧЕ ![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА