Повторение курса 7 класса Четырёхугольники Параллелограмм и его свойства Трапеция Площади Теорема Пифагора Подобные треугольники. Признаки подобия треугольников Пропорциональные отрезки в прямоугольных треугольниках Соотношение между сторонами и углами прямоугольного треугольника Окружность. Касательная к окружности Центральные и вписанные углы Четыре замечательные точки треугольника Вписанная и описанная окружности

 

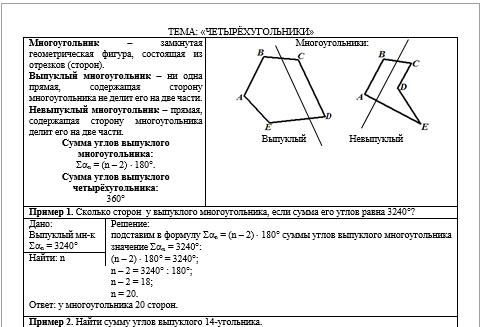
"Четырёхугольники".

 

После изучения этой темы:

Перед началом обучения обязательно распечатайте материал для работы (нажмите на изображение ниже):

 

Дополнительные материалы: "Многоугольники" (презентация)

Обратите внимание!

 

В левом столбце печатного материала находятся:

  • краткая теория по теме.

В правом столбце печатного материала находятся:

  • графические иллюстрации к теоретическому материалу.

Материал содержит три разобранные задачи и три задачи предложено решить самостоятельно.

 

 
Печатный материал содержит две страницы, которые выглядят так:
Пример 1. Сколько сторон у выкуклого многоугольника, если сумма его углов равна 3240о?

Рядом с условием запишем слово "Решение:"

Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

 

 

Подставим в формулу суммы углов выпуклого многоугольника значение суммы углов - 3240о:

 

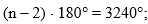
Решим уравнение:

 

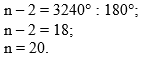
Запишем ответ к задаче:

Пример 2. Найти сумму углов выпуклого 14-угольника.

Рядом с условием запишем слово "Решение:"

Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

 

 

Подставим в формулу суммы углов выпуклого многоугольника значение количества углов - n = 14:

 

Запишем ответ к задаче:

Пример 3. Найти сумму углов выпуклого 14-угольника.

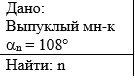Рядом с условием запишем слово "Решение:"

Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

 

 

По формуле суммы углов выпуклого многоугольника

 

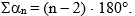
Т.к. в многоугольнике n углов, то

 

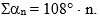
Приравняем правые части полученных равенств:

 

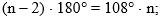
Решим получившееся уравнение:

 

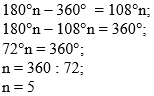
Запишем ответ к задаче:

ВЕРНУТЬСЯ НАВЕРХ ВЕРНУТЬСЯ К ПРИМЕРУ 1 ВЕРНУТЬСЯ К ПРИМЕРУ 2 ВЕРНУТЬСЯ К ПРИМЕРУ 3 ПЕЧАТЬ МАТЕРИАЛА

©Материал подготовлен учителем математики Максимовской Мариной Алексеевной