Повторение курса 7 класса Четырёхугольники Параллелограмм и его свойства Трапеция Площади Теорема Пифагора Подобные треугольники. Признаки подобия треугольников Пропорциональные отрезки в прямоугольных треугольниках Соотношение между сторонами и углами прямоугольного треугольника Окружность. Касательная к окружности Центральные и вписанные углы Четыре замечательные точки треугольника Вписанная и описанная окружности 

 

"Пропорциональные отрезки в прямоугольных треугольниках".

 

После изучения этой темы:

Перед началом обучения обязательно распечатайте материал для работы (нажмите на изображение ниже):

 

Дополнительные материалы: "Пропорциональные отрезки в прямоугольном треугольнике" (презентация)

Обратите внимание!

 

В левом столбце печатного материала находятся:

  • теоретические материалы;

  • краткая запись теоретических положений.

В правом столбце печатного материала находятся:

  • графическая иллюстрация к теоретическому материалу.

Материал содержит три разобранных задачи и девять задач предложено решить самостоятельно.
Печатный материал содержит две страницы, которые выглядят так:
Пример 1. По данным рисунка докажите АС, ВС, НВ и АВ.

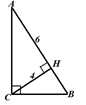Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

В первом действии воспользуемся теоремой Пифагора для прямоугольного треугольника  АСН и найдём его гипотенузу АС:

Во втором действии рассмотрим прямоугольный треугольник АВС с высотой СН. Высота СН является средним пропорциональным между отрезками, на которые основание высоты - точка Н - делит гипотенузу, подставим длину СН и АН и найдём НВ:

В третьем действии гипотенузу АВ прямоугольного треугольника АВС:

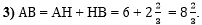В четвёртом действии рассмотрим прямоугольный треугольник ВСН (в нём гипотенуза СВ) и по теореме Пифагора найдем СВ:

Теперь напишем ответ к задаче: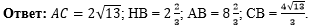

Пример 2. По данным рисунка найдите KN, KM, KF.

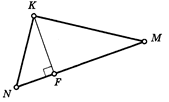Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

В первом действии из условия, что KN : KM = 3 : 4, выразим, например, KN через KM:

Во втором действии рассмотрим прямоугольный треугольник KNM с гипотенузой MN. Воспользуемся теоремой Пифагора, подставим вместо катета KN выражение, полученное в первом действии:

,

затем решим полученное уравнение и найдём КМ:

,

а затем подставим полученное значение КМ в выражение, полученное в первом действии:

В третьем действии в том же прямоугольном треугольнике KNM воспользуемся тем, что катет КN - среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

,

затем подставим вместо КN и NM их длины, решим получившееся уравнение, найдём NF, а затем вычислим FM:

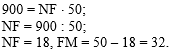В четвёртом действии воспользуемся тем, что высота KF - среднее пропорциональное между отрезками, на которые точка F делит гипотенузу NM:

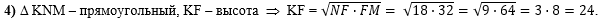Теперь напишем ответ к задаче:

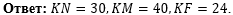Пример 3. По данным найдите площадь параллелограмма ABCD.

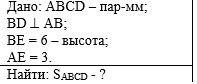Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

В первом действии в прямоугольном треугольнике ABD воспользуемся тем, что высота ВЕ - среднее пропорциональное между отрезками, на которые эта высота делит гипотенузу AD, решим получившееся уравнение и найдём отрезок ED:

Во втором действии вычислим сторону AD параллелограмма ABCD:

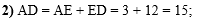В третьем действии найдём площадь параллелограмма ABCD как произведение стороны AD на высоту BE:

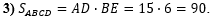Теперь напишем ответ к задаче:

ВЕРНУТЬСЯ НАВЕРХ ВЕРНУТЬСЯ К ПРИМЕРУ 1  ВЕРНУТЬСЯ К ПРИМЕРУ 2 ВЕРНУТЬСЯ К ПРИМЕРУ 3 ПЕЧАТЬ МАТЕРИАЛА

©Материал подготовлен учителем математики Максимовской Мариной Алексеевной