Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
Обратите внимание!
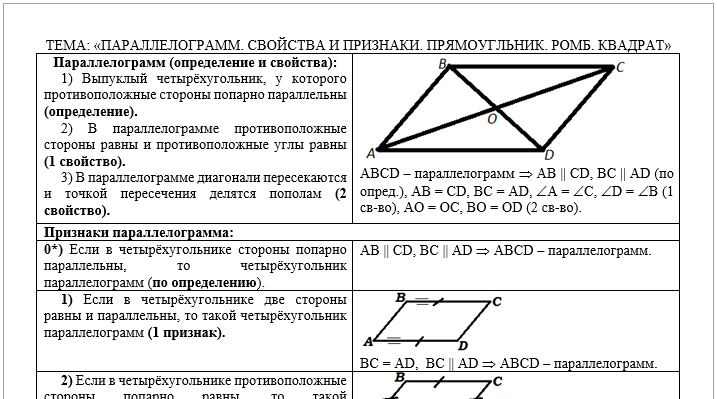
В левом
столбце печатного материала находятся:
В правом
столбце печатного материала находятся:
Материал
содержит 4 разобранных задачи, 10 задач предлагается для
самостоятельного решения
|
 |
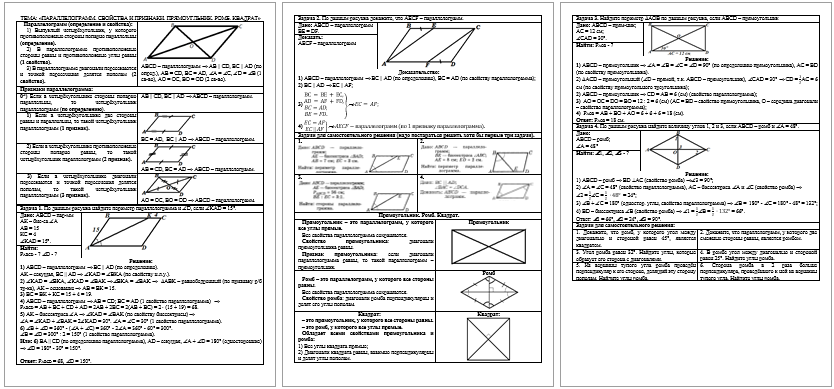
| Печатный
материал содержит три страницы, которые выглядят так: |
 |
|
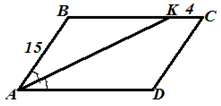
Задача 1. По данным рисунка
найдите периметр параллелограмма и угол D,
если угол KAD = 15o. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
используем условие, что АBСD -
параллелограмм, следовательно BC параллельна
AD (по определению параллелограмма):

Далее используем свойство параллельных прямых BC
и AD, пересечённых секущей
AK - накрест лежащие углы KAD и
BKA равны:
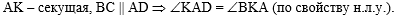 , ,
|
|
Во втором действии
используем условие, что углы KAD и
BKA равны (из 1)) и углы KAD и
BAK равны (по условию):
 , ,
Из равенства углов
BKA и ВАК следует, что
треугольник АВК - равнобедренный с основанием АК, по признаку
равнобедренного треугольника:
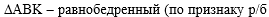 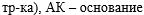 , ,
откуда следует, что стороны АВ и ВК равны:
 |
|
В третьем действии
находим сторону ВС из условия, что ВС = ВК + КС:
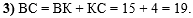 , ,
|
|
В четвёртом действии,
из условия, что ABCD - параллелограмм и
противоположные стороны параллелограмма равны (по свойству
параллелограмма), выведем формулу для вычисления периметра и вычислим
его:
 |
|
В пятом действии
воспользуемся условием, что АК - биссектриса угла А (углы
KAD и BAK - равны) и
свойством параллелограмма, что противоположные углы равны (угол А равен
углу С):
 . .
|
|
В шестом действии
можно воспользоваться тем, что сумма углов параллелограмма равна 360о,
противоположные углы (углы
B и D) равны:
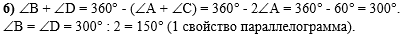
или свойством односторонних
углов параллелограмма:
 |
Напишем ответ к задаче:
 |
|
Задача 2. По данным рисунка
докажите, что AECF -
параллелограмм |
|
 |
 |
Общий вид решения задачи:
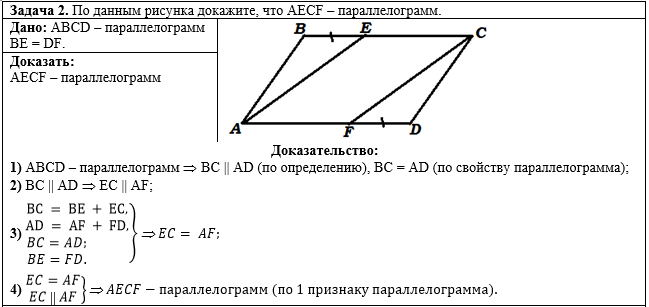
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Доказательство:" |
|
В первом действии
используем условие, что АBСD -
параллелограмм, следовательно BC параллельна
AD (по определению параллелограмма) и ВС =
AD (по свойству параллелограмма):
 |
|
Во втором действии
используем полученный вывод (ВС параллельна AD)
и получим, что EC параллельна
AF (т.к. они лежат на сторонах ВС и
AD соответственно:
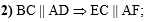
|
|
В третьем действии
используем равенство сторон AD и ВС (по
свойству параллелограмма), равенство отрезков BE
и FD (по условию) и сделаем вывод, что ЕС =
AF:
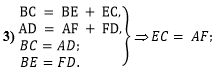 , ,
|
|
В четвёртом действии
соберём то, что относится к первому признаку параллелограмма (две
стороны четырёхугольника параллельны и равны), и докажем, что
AECF - параллелограмм:
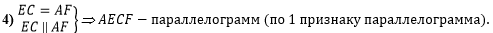 |
|
Задача 3. По данным рисунка найти
периметр треугольника АОВ, если ABCD -
прямоугольник. |
|
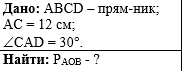 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
используем условие, что АBСD -
прямоугольник, следовательно, все углы у него прямые и диагонали
AC и BD равны (по
определению и свойству прямоугольника):
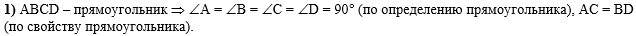 |
|
Во втором действии
свойством катета прямоугольного треугольника ACD,
лежащего против угла CAD = 30о (он
равен половине гипотенузы АС):
 , ,
|
|
В третьем действии
воспользуемся равенством противоположных сторон прямоугольника:
 , ,
|
|
В четвёртом действии
воспользуемся свойством равенства диагоналей прямоугольника и тем, что
диагонали параллелограмма точкой пересечения диагоналей делится пополам:
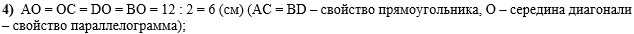 |
|
В пятом действии
найдём периметр треугольника АОВ:
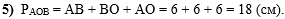 . .
|
Напишем ответ к задаче:
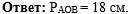 |
|
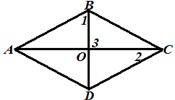
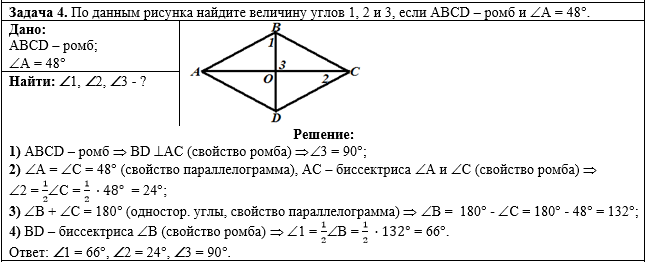
Задача 4. По данным рисунка
найдите величины углов 1, 2 и 3, если
ABCD - ромб и угол А =
48o. |
|
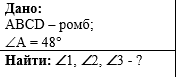 |
 |
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
используем условие, что АBСD -
ромб, следовательно BD перпендикулярна
AС (по свойству ромба), тогда угол 3 - прямой:
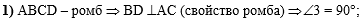 |
|
Во втором действии
воспользуемся равенством противоположных углов параллелограмма (угол А
равен углу С) и тем, что АС - биссектриса углов А и С (свойство ромба).
Найдём угол 2:
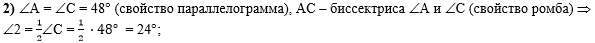 , ,
|
|
В третьем действии
из свойства односторонних углов параллелограмма найдём угол В:
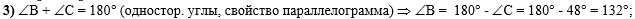 , ,
|
|
В четвёртом действии
по свойству ромба (диагональ BD - биссектриса
угла В) найдём угол 1:
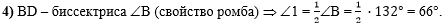 |
Напишем ответ к задаче:
 |
![]() Повторение
курса 7 класса
Повторение
курса 7 класса
![]() Четырёхугольники
Четырёхугольники
![]() Параллелограмм
и его свойства
Параллелограмм
и его свойства
![]() Трапеция
Трапеция
![]() Площади
Площади
![]() Теорема
Пифагора
Теорема
Пифагора
![]() Подобные
треугольники. Признаки подобия треугольников
Подобные
треугольники. Признаки подобия треугольников
![]() Пропорциональные
отрезки в прямоугольных треугольниках
Пропорциональные
отрезки в прямоугольных треугольниках
![]() Соотношение
между сторонами и углами прямоугольного треугольника
Соотношение
между сторонами и углами прямоугольного треугольника
![]() Окружность.
Касательная к окружности
Окружность.
Касательная к окружности
![]() Центральные
и вписанные углы
Центральные
и вписанные углы
![]() Четыре
замечательные точки треугольника
Четыре
замечательные точки треугольника
![]() Вписанная
и описанная окружности
Вписанная
и описанная окружности
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 1
ВЕРНУТЬСЯ К ЗАДАЧЕ 1
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 2
ВЕРНУТЬСЯ К ЗАДАЧЕ 2
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 3
ВЕРНУТЬСЯ К ЗАДАЧЕ 3
![]() ВЕРНУТЬСЯ К ЗАДАЧЕ 4
ВЕРНУТЬСЯ К ЗАДАЧЕ 4 ![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА