Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
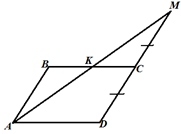
Пример 1. По данным рисунка докажите, что
площадь параллелограмма ABCD равна площади
треугольника AMD. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Доказательство:" |
|
В первом действии,
т.к. параллелограмм ABCD разделён на две
фигуры - треугольник АВК и трапецию AKCD, по
второму свойству площадей сделаем вывод, что площадь параллелограмма
ABCD также равна сумме площадей треугольника
АВК и трапеции AKCD:
 , ,
|
|
Во втором действии,
т.к. треугольник AMD состоит из треугольника
КМС и трапеции AKCD,
по второму свойству площадей сделаем вывод, что площадь треугольника
AMD также равна сумме площадей треугольника
КМС и трапеции AKCD:
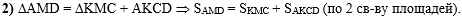 , ,
|
|
В третьем действии,
используя свойство противоположных сторон параллелограмма и условие
задачи, докажем, что отрезки АВ и МС равны:
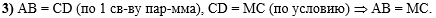 , ,
|
|
В четвёртом действии,
зная, что противоположные стороны параллелограмма параллельны по
определению, и свойства накрест лежащих углов при пересечении
параллельных прямых секущей, докажем, что равны углы КМС и КАВ, а также
углы КСМ и КВА:
 |
|
В пятом действии
объединяем то, что доказали в третьем и четвёртом действии и докажем,
что треугольники АВК и КМС равны (по второму признаку равенства
треугольников), откуда сделаем вывод, что и площади этих треугольников
равны (по первому свойству площадей):
 ; ;
|
|
В шестом действии
объединяем выводы, полученные в первом, втором и пятом действиях, и
доказываем, что площадь параллелограмма ABCD
равна площади треугольника AMD:
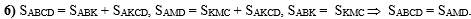 |
|
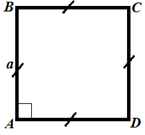
Пример 2.
а) найдите площадь квадрата со стороной 13√5 мм; б) найдите сторону
квадрата, если его площадь составляет 675 м2. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем "а) Решение:" |
|
а) зная, что площадь
квадрата равна квадрату его стороны (третье свойство площадей), найдём
площадь квадрата ABCD:
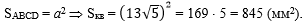 , ,
|
|
Ниже запишем: "б)
Решение:"
|
|
б) зная формулу
площади квадрата, выразим сторону квадрата через его площадь и найдём
эту сторону:
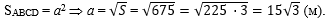 , ,
|
|
Осталось написать ответ к
задаче: 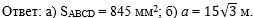 |
|
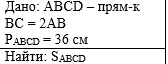
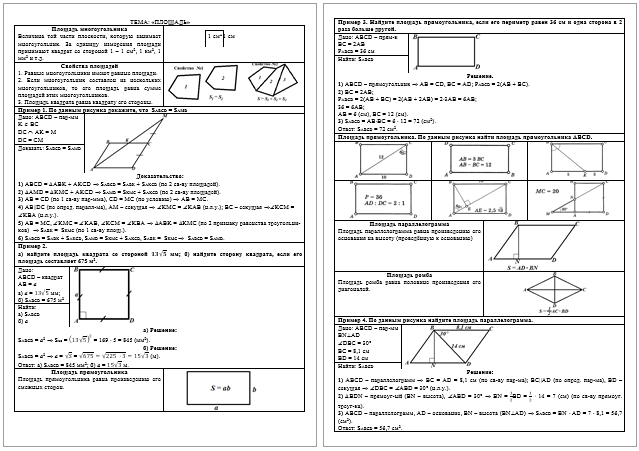
Пример 3.
Найдите площадь прямоугольника, если его периметр
равен 36 см и одна сторона в 2 раза больше другой. |
|
 |
 |
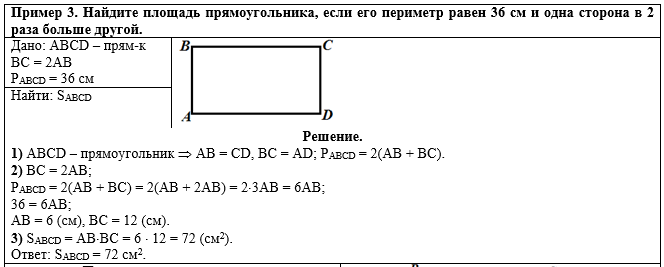
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии из
того, что ABCD является прямоугольником
сделаем вывод, что противоположные стороны равны, а, следовательно,
периметр прямоугольника равен удвоенной сумме смежных сторон:
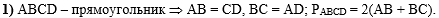 , ,
|
|
Во втором действии
используем условие, что сторона ВС в 2 раза больше стороны АВ, подставим
его в формулу периметра прямоугольника, затем получим уравнение,
подставив значение периметра 36 см, и, решив полученное уравнение,
найдём сторону АВ, а затем - сторону ВС:
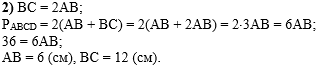 , ,
|
|
В третьем действии,
используя найденные длины сторон прямоугольника ABCD,
найдём площадь, как произведение его смежных сторон:
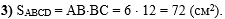
Осталось написать ответ к задаче:

|
|
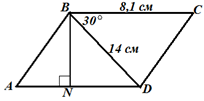
Пример 4. По данным рисунка
найдите площадь параллелограмма. |
|
 |
 |
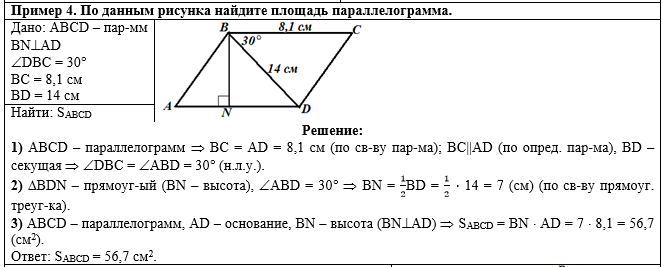
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии,
т.к. ABCD - параллелограмм, из равенства
противоположных сторон параллелограмма найдём сторону
AD, а из условия, что противоположные стороны параллелограмма
параллельны (по определению параллелограмма), а диагональ
BD является секущей, сделаем вывод, что угол
ABD равен углу DBC
как накрест лежащие углы:
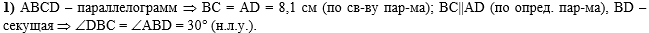 , ,
|
|
Во втором действии
рассмотрим прямоугольный треугольник AВD
(BN перпендикулярен AD),
воспользуемся свойством катета, лежащего против угла 30 градусов, найдём
BN - высоту параллелограмма
ABCD:
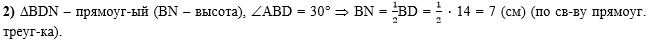 , ,
|
|
В третьем действии
найдём площадь параллелограмма ABCD, как
произведение стороны параллелограмма на высоту, проведённую к этой
стороне:
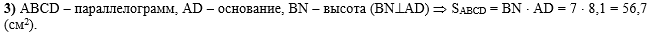
Теперь остаётся написать к задаче ответ:
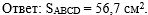
|
|
Пример 5. По данным рисунка
найдите высоту СМ, проведённую к стороне АВ
треугольника АВС. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
проведём высоту СМ:
 ,
обратите внимание на запись в квадратных скобках - её в решении делать
не нужно, также, как и рисовать второй рисунок. Это дополнительное
построение делаем на том рисунке, который выполнен к задаче. ,
обратите внимание на запись в квадратных скобках - её в решении делать
не нужно, также, как и рисовать второй рисунок. Это дополнительное
построение делаем на том рисунке, который выполнен к задаче.
|
|
Во втором действии
рассмотрим прямоугольный треугольник АВН (т.к. ВН является высотой
треугольника АВС, следовательно, ВН перпендикулярна АС) и по свойству
катета, лежащего против угла 30 градусов, найдём высоту ВН:

|
|
В третьем действии
найдём площадь треугольника АВС как половину произведения стороны АС на
высоту ВН, проведённую к ней:
 |
|
В четвёртом действии
выразим площадь треугольника АВС через сторону АВ и высоту СМ,
проведённую к этой стороне, подставим найденное в третьем действии
значение площади и, решив полученное уравнение, найдём высоту СМ:

Осталось написать ответ к задаче:

|
|
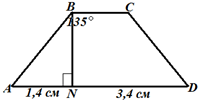
Пример 6. По данным рисунка
найдите площадь равнобедренной трапеции ABCD. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
сделаем вывод из того, что если ABCD -
равнобедренная трапеция, ВС, AD - основания,
то АВ = CD как боковые стороны равнобедренной
трапеции:
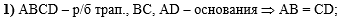
|
|
Во втором действии
найдём длину основания AD:

|
|
В третьем действии,
используя свойство односторонних углов при основаниях трапеции, найдём
угол А:
 , ,
|
|
В четвёртом действии
рассмотрим прямоугольный треугольник ABN (BN
перпендикулярна AD как высота трапеции)
и, пользуясь свойством острых углов прямоугольного треугольника (их
сумма равна 90 градусам), найдём угол ABN.
Угол ABN равен углу А, откуда можно сделать
вывод, что прямоугольный треугольник ABN
является равнобедренным, следовательно AN = BN =
1,4 см:
 |
|
В пятом действии
проведём высоту СР и получим прямоугольный треугольник
CPD:
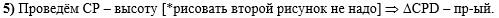
Обратите внимание, что дополнительное построение достаточно выполнить на
том же рисунке, который нарисован к задаче, рисовать второй рисунок и
делать запись об этом не нужно!
|
|
В шестом действии
докажем, что прямоугольные треугольники ABN и
CPD равны (по гипотенузе (AB
= CD) и острому углу (угол А равен углу D),
откуда сделаем вывод, что PD = AN:
 |
|
В седьмом действии
рассмотрим прямоугольник NBCP (т.к.
BN и CP - высоты
трапеции, ВС параллельна NP, то все углы этого
четырёхугольника прямые), в котором противоположные стороны
BC и NP равны и
NP можно вычислить, как разность
ND и PD:
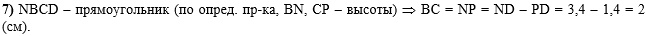 |
|
В восьмом действии
найдём площадь трапеции ABCD как произведение
половины суммы оснований трапеции на её высоту:
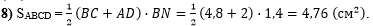
Осталось написать ответ к
задаче:
 |
![]() Повторение
курса 7 класса
Повторение
курса 7 класса
![]() Четырёхугольники
Четырёхугольники
![]() Параллелограмм
и его свойства
Параллелограмм
и его свойства
![]() Трапеция
Трапеция
![]() Площади
Площади
![]() Теорема
Пифагора
Теорема
Пифагора
![]() Подобные
треугольники. Признаки подобия треугольников
Подобные
треугольники. Признаки подобия треугольников
![]() Пропорциональные
отрезки в прямоугольных треугольниках
Пропорциональные
отрезки в прямоугольных треугольниках
![]() Соотношение
между сторонами и углами прямоугольного треугольника
Соотношение
между сторонами и углами прямоугольного треугольника
![]() Окружность.
Касательная к окружности
Окружность.
Касательная к окружности
![]() Центральные
и вписанные углы
Центральные
и вписанные углы
![]() Четыре
замечательные точки треугольника
Четыре
замечательные точки треугольника
![]() Вписанная
и описанная окружности
Вписанная
и описанная окружности

![]() ВЕРНУТЬСЯ К ПРИМЕРУ 1
ВЕРНУТЬСЯ К ПРИМЕРУ 1
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 2
ВЕРНУТЬСЯ К ПРИМЕРУ 2
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 3
ВЕРНУТЬСЯ К ПРИМЕРУ 3
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 4
ВЕРНУТЬСЯ К ПРИМЕРУ 4
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 5
ВЕРНУТЬСЯ К ПРИМЕРУ 5
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 6
ВЕРНУТЬСЯ К ПРИМЕРУ 6
![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА