Повторение курса 7 класса Четырёхугольники Параллелограмм и его свойства Трапеция Площади Теорема Пифагора Подобные треугольники. Признаки подобия треугольников Пропорциональные отрезки в прямоугольных треугольниках Соотношение между сторонами и углами прямоугольного треугольника Окружность. Касательная к окружности Центральные и вписанные углы Четыре замечательные точки треугольника Вписанная и описанная окружности

 

"Соотношение между сторонами и углами прямоугольного треугольника".

 

После изучения этой темы:

Перед началом обучения обязательно распечатайте материал для работы (нажмите на изображение ниже):

 

Дополнительные материалы: "Соотношение углов и сторон в прямоугольном треугольнике" (презентация)

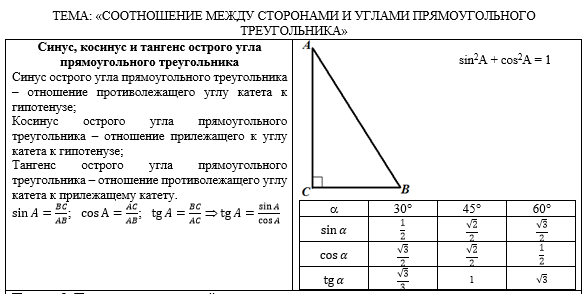
Обратите внимание!

 

В левом столбце печатного материала находятся:

  • теоретический материал;

  • краткая запись определений синуса, косинуса и тангенса острого угла прямоугольного треугольника.

В правом столбце печатного материала находятся:

  • графическая иллюстрация к теоретическому материалу;

  • таблица значений тригонометрических функций некоторых углов;

  • формулу основного тригонометрического тождества.

Материал содержит пять разобранных задач и девять задач предлагается для самостоятельного решения.
Печатный материал содержит две страницы, которые выглядят так:
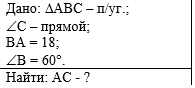
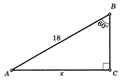
Пример 1. По данным рисунка найдите х.

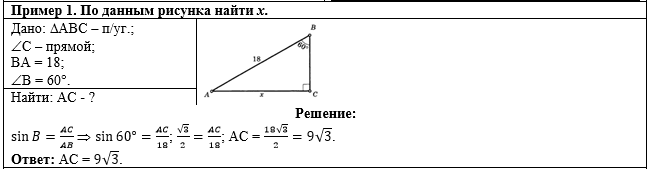
Общий вид решения задачи:

 

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

В решении используем определение синуса острого угла - выразим синус угла В через противолежащий катет АС и гипотенузу АВ прямоугольного треугольника АВС. Значение синуса 60 градусов возьмём из таблицы значений тригонометрических функций некоторых углов:

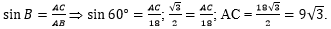Напишем ответ к задаче:

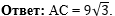
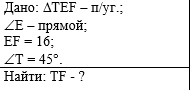
Пример 2. По данным рисунка найдите х.

Общий вид решения задачи:

 

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

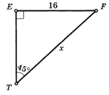
В решении используем определение синуса острого угла - выразим синус угла Т через противолежащий катет EF и гипотенузу TF прямоугольного треугольника TEF. Значение синуса 45 градусов возьмём из таблицы значений тригонометрических функций некоторых углов:

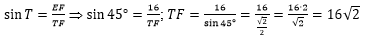Напишем ответ к задаче:

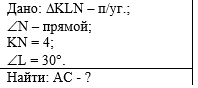
Пример 3. По данным рисунка найдите х.

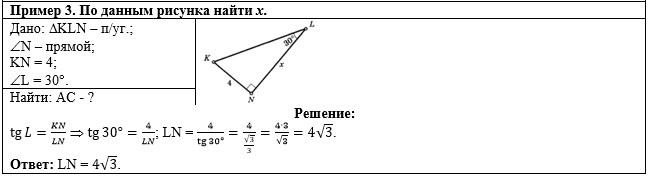
Общий вид решения задачи:

 

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

В решении используем определение тангенса острого угла - выразим тангенс угла L через противолежащий катет KN и прилежащий катет LN прямоугольного треугольника KLN. Значение тангенса 30 градусов возьмём из таблицы значений тригонометрических функций некоторых углов:

Напишем ответ к задаче:

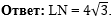
Пример 4. Найдите площадь параллелограмма MPKN.

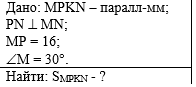Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

В первом действии из того, что PN и MN перпендикулярны, сделаем вывод, что PN - высота параллелограмма MPKN:

Во втором действии рассмотрим прямоугольный треугольник MPN с гипотенузой МР:

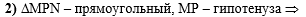, следовательно, можно воспользоваться сначала определением синуса острого угла - выразить синус угла М через противолежащий катет PN и гипотенузу МР и найти далее катет PN:

,

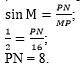а затем воспользоваться определением косинуса острого угла - выразить косинус угла М через прилежащий катет MN и гипотенузу МР и найти катет MN:

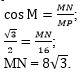В третьем действии найдём площадь параллелограмма MPKN как произведение высоты PN на сторону MN, к которой эта высота проведена:

Осталось написать ответ к задаче: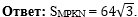

Пример 5. По данным рисунка найдите АВ, ВС и АС.

Общий вид решения задачи:

Слева напишем краткое условие задачи, используя условные обозначения.

С правой стороны от краткого условия разместим рисунок, на котором отмечены данные задачи.

Под условием и рисунком запишем слово "Решение:"

В первом действии рассмотрим прямоугольный треугольник ABD с гипотенузой AB:

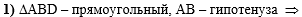, следовательно, можно воспользоваться сначала определением синуса острого угла - выразить синус угла А через противолежащий катет BD и гипотенузу AB и найти далее гипотенузу AB:

,

а затем воспользоваться определением косинуса острого угла - выразить косинус угла A через прилежащий катет AD и гипотенузу AB и найти катет AD:

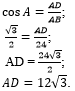Во втором действии рассмотрим прямоугольный треугольник CBD с гипотенузой CB:

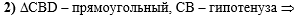, следовательно, можно воспользоваться сначала определение синуса острого угла - выразить синус угла C через противолежащий катет BD и гипотенузу BC и найти далее гипотенузу BC:

,

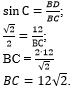а затем воспользоваться определением косинуса острого угла - выразить косинус угла С через прилежащий катет DC и гипотенузу BC и найти катет DC:

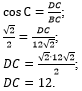В третьем действии найдём сторону АС треугольника АВС:

Осталось написать ответ к задаче:

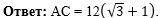ВЕРНУТЬСЯ НАВЕРХ ВЕРНУТЬСЯ К ПРИМЕРУ 1  ВЕРНУТЬСЯ К ПРИМЕРУ 2 ВЕРНУТЬСЯ К ПРИМЕРУ 3 ВЕРНУТЬСЯ К ПРИМЕРУ 4 ВЕРНУТЬСЯ К ПРИМЕРУ 5 ПЕЧАТЬ МАТЕРИАЛА

©Материал подготовлен учителем математики Максимовской Мариной Алексеевной