Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
Пример 1. Докажите, что
биссектриса треугольника делит противоположную сторону на отрезки,
пропорциональные прилежащим сторонам треугольника. |
|
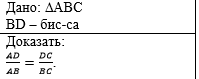 |
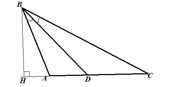 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Доказательство:" |
|
В первом действии
отметим, что биссектриса делит треугольник АВС на два треугольника:
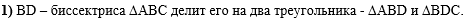
|
|
Во втором действии
построим ВН - общую высоту этих треугольников, следовательно, по
свойству площадей треугольников, имеющих равную высоту, отношение
площадей таких треугольников равно отношению основанию этих
треугольников:
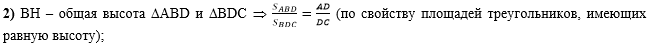 Ссылка
на материал
"Площади" (см. стр. 3) Ссылка
на материал
"Площади" (см. стр. 3)
|
|
В третьем действии
воспользуемся свойством площадей треугольников, имеющих равные углы -
отношение площадей таких треугольников равно отношению произведений
сторон, содержащих эти углы:
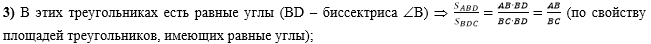 Ссылка
на материал
"Площади" (см. стр. 3) Ссылка
на материал
"Площади" (см. стр. 3) |
|
В четвёртом действии
объединим выводы, полученные во 2 и в 3 действиях, а затем воспользуемся
основным свойством пропорции - можно поменять местами средние члены
пропорции, после чего получим вывод, что отношения отрезка
AD к АВ равно отношению отрезка
DC к ВС, т.к. отрезки являются
пропорциональными по определению пропорциональных отрезков:
 |
|
Пример 2. Площади двух подобных
треугольников 75 м2 и 300 м2. Одна из сторон
второго треугольника 9 м, найдите сходственную ей сторону первого
треугольника. |
|
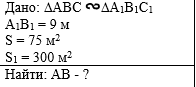 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
воспользуемся свойством подобных треугольников, что отношение их
площадей равно квадрату коэффициента подобия треугольников, и найдём
этот коэффициент:

|
|
Во втором действии
зная, что отношение сходственных сторон подобных треугольников равно
коэффициенту подобия, подставим в это отношение значение коэффициента и
длину известной стороны А1В1 и найдём длину
стороны АВ:

|
|
Осталось написать ответ к
задаче: 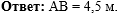 |
|
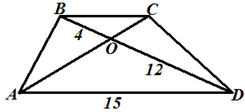
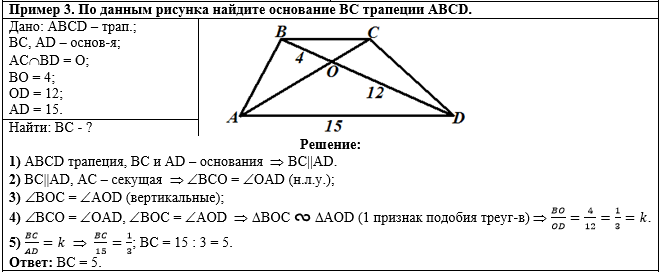
Пример 3. По данным рисунка
найдите основание ВС трапеции АВСD. |
|
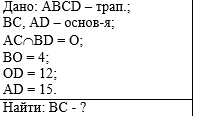 |
 |
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
из условия, что ABCD - трапеция, ВС и
AD - её основания, сделаем вывод, что ВС
параллельна AD (по определению трапеции):

|
|
Во втором действии
рассмотрим параллельные прямые BC и
AD и секущую АС, откуда следует (по свойству
накрест лежащих углов при параллельных прямых и секущей), что углы ВСО и
OAD равны:
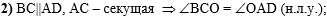
|
|
В третьем действии
отметим, что углы ВОС и AOD равны как
вертикальные:
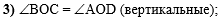 |
|
В четвёртом действии
докажем, что треугольники ВОС и AOD подобны по
1 признаку подобия треугольников (по двум соответственно равным углам),
а, следовательно, отношение сходственных сторон ВО и
OD равно коэффициенту подобия:
 |
|
В пятом действии,
зная, что треугольники ВОС и AOD подобны и
отношение двух их сходственных сторон ВС и AD
также равно коэффициенту подобия, подставим в это отношение длину
основания AD и получим длину стороны ВС:

Осталось написать ответ к задаче:
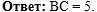 |
|
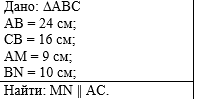
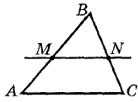
Пример 4. По данным рисунка
докажите, что MN параллельна АС. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Доказательство:" |
|
В первом действии,
зная АВ и АМ, найдём длину МВ:
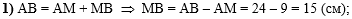
|
|
Во втором действии
зная, что угол В общий угол треугольников BMN
и АВС, найдём отношение сходственных сторон и убедившись, что они равны,
докажем, что треугольники BMN и АВС подобны по
2 признаку подобия:

|
|
В третьем действии
зная, что треугольники BMN и АВС подобны,
сделаем вывод, что соответственные углы BMN и
ВАС равны:
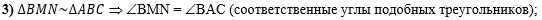 |
|
В четвёртом действии
докажем параллельность прямых
MN и АС по второму признаку параллельности
прямых (при пересечении двух прямых MN и АС
секущей АВ соответственные углы равны):
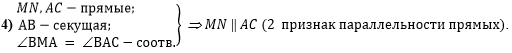 |
|
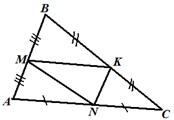
Пример 5. По данным рисунка
найдите периметр треугольника АВС, если периметр треугольника
MNK равен 67 м. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
из условия, что М и N - середины сторон АВ и
АС соответственно, сделаем вывод, что MN -
средняя линия треугольника АВС, а, следовательно, MN
равна половине ВС:

|
|
Во втором действии
аналогично первому действию получим, что МК - половина АС и
KN - половина АВ:
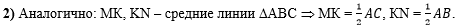
|
|
В третьем действии
сначала в общем виде запишем периметр треугольника
MNK, как сумму сторон MN, NK и
MK, затем подставим вместо этих сторон выражения, полученные в
первом и втором действии, вынесем общий множитель 1/2 и увидим, что
внутри сумма длин сторон АВ, ВС и АС, т.к. - периметр треугольника АВС.
Таким образом, периметр треугольника АВС в два
раза больше периметра треугольника MNK. Дальше
просто подставим в полученное равенство значение периметра треугольника
MNK и получим периметр треугольника АВС:
 |
|
Осталось написать ответ к задаче:
 |
|
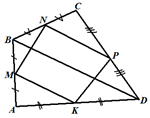
Пример 6. Докажите по данным
рисунка, что четырёхугольник MNKP -
параллелограмм. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Доказательство:" |
|
В первом действии
проведём диагональ BD, т.к.
N и Р - середины сторон ВС и CD
соответственно, следовательно, NP - средняя
линия треугольника BCD, откуда по свойству
средней линии треугольника сделаем вывод, что отрезок
NP параллелен BD и
равен его половине:

|
|
Во втором действии
т.к. М - середина ВА, а К - середина AD, то МК
- средняя линия треугольника ABD, а,
следовательно, отрезок МК параллелен BD и
равен его половине:

|
|
В третьем действии
покажем, что NP и MK
равны, так как равны половине BD:
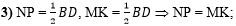 |
|
В четвёртом действии
покажем, что NP и MK
параллельны, так как оба параллельны BD:
 |
|
В пятом действии
объединим выводы, полученные в третьем и четвёртом действии, докажем,
что MNPK - параллелограмм по 1 признаку
параллелограмма:
 |
|
Пример 7. В треугольнике АВС
медианы АА1 и ВВ1 пересекаются в точке О. Найдите
площадь треугольника АВС, если площадь треугольника АВО равна 16 см2. |
|
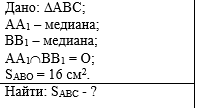 |
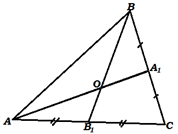 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
из условия, что медианы АА1 и ВВ1 пересекаются в точке О сделаем вывод,
что отношение АО к ОА1 равно отношению ВО к ОВ1 и равно 2 : 1 (по
свойству медиан треугольника):
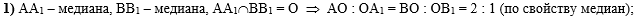
|
|
Во втором действии
проведём медиану СС1. По свойству медиан треугольника она пройдёт через
точку О, и также отношение СО к ОС1 будет равно 2 : 1:

|
|
В третьем действии
СН параллельно стороне АВ:
 |
|
В четвёртом действии
проведём отрезок НН1 перпендикулярно АВ через точку О. НН1 будет
перпендикулярен и прямой СН, т.к. СН параллельна АВ по построению. Тогда
(по определению расстояния между параллельными прямыми) НН1 - расстояние
между прямыми СН и АВ, а также будет расстоянием между точкой С и прямой
АВ, т.е. высотой треугольника АВС, проведённой к стороне АВ:
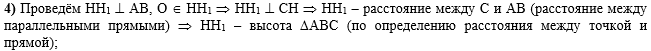 |
|
В пятом действии
зная, что ОН1 перпендикулярен АВ, сделаем вывод, что ОН1 - высота
треугольника АВО:
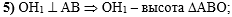 |
|
В шестом действии,
применив для каждого треугольника АВС и АВО формулу площади
треугольника, найдём отношение их площадей, сократим дробь на общие
множители 1/2 и АВ и получим, что отношение площадей треугольников АВС и
АВО равно отношению их высот НН1 и ОН:
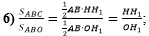 |
|
В седьмом действии
рассмотрим прямоугольные треугольники ОСН и ОС1Н1 и докажем их подобие
по 1 признаку подобия. Далее, зная, что отношение сходственных сторон СО
и ОС1 равно 2 : 1, получаем, что отношение НО к ОН1 тоже равно 2 : 1, а
следовательно, весь отрезок НН1 в три раза больше отрезка ОН1:
 |
|
В восьмом действии
подставим в отношение, полученное в 6 действии, вместо НН1 выражение
3ОН1, сократим дробь на общий множитель ОН1 и получим, что площадь
треугольника АВС в три раза больше площади треугольника АВО, после чего
найдём площадь треугольника АВС:
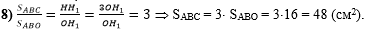
Осталось написать ответ к задаче:
 |
![]() Повторение
курса 7 класса
Повторение
курса 7 класса
![]() Четырёхугольники
Четырёхугольники
![]() Параллелограмм
и его свойства
Параллелограмм
и его свойства
![]() Трапеция
Трапеция
![]() Площади
Площади
![]() Теорема
Пифагора
Теорема
Пифагора
![]() Подобные
треугольники. Признаки подобия треугольников
Подобные
треугольники. Признаки подобия треугольников
![]() Пропорциональные
отрезки в прямоугольных треугольниках
Пропорциональные
отрезки в прямоугольных треугольниках
![]() Соотношение
между сторонами и углами прямоугольного треугольника
Соотношение
между сторонами и углами прямоугольного треугольника
![]() Окружность.
Касательная к окружности
Окружность.
Касательная к окружности
![]() Центральные
и вписанные углы
Центральные
и вписанные углы
![]() Четыре
замечательные точки треугольника
Четыре
замечательные точки треугольника
![]() Вписанная
и описанная окружности
Вписанная
и описанная окружности



![]() ВЕРНУТЬСЯ К ПРИМЕРУ 1
ВЕРНУТЬСЯ К ПРИМЕРУ 1 ![]() ВЕРНУТЬСЯ К ПРИМЕРУ 2
ВЕРНУТЬСЯ К ПРИМЕРУ 2
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 3
ВЕРНУТЬСЯ К ПРИМЕРУ 3
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 4
ВЕРНУТЬСЯ К ПРИМЕРУ 4
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 5
ВЕРНУТЬСЯ К ПРИМЕРУ 5
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 6
ВЕРНУТЬСЯ К ПРИМЕРУ 6
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 7
ВЕРНУТЬСЯ К ПРИМЕРУ 7
![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА