Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
Обратите внимание!
В левом
столбце печатного материала находятся:
В правом
столбце печатного материала находятся:
Материал
содержит четыре разобранных задачи и три задачи предложено решить
самостоятельно.
|
 |
| Печатный
материал содержит две страницы, которые выглядят так: |
 |
|
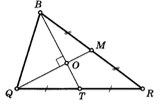
Пример 1. По данным рисунка
найдите площадь треугольника BOQ, если
QM = 9, ВТ = 12. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
используем условие, что QM и ВТ - медианы - по
свойству медиан треугольника сделаем вывод, что и точка пересечения О
делит медианы в отношении 2 : 1:
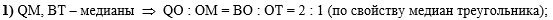
|
|
Во втором действии
зная длину QM и то, что QO
: OM = 2 : 1, найдём длину отрезка QO:
 |
|
В третьем действии
зная длину ВТ и то, что ВО : ОТ = 2 : 1, найдём длину отрезка ВО:
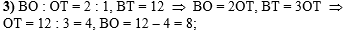 |
|
В четвёртом действии,
зная, что QM и ВТ перпендикулярны,
делаем вывод, что треугольник BQM -
прямоугольный, тогда можно найти площадь прямоугольного треугольника
BQM как половину произведения его катетов:
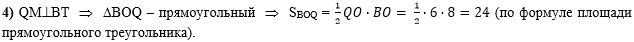 |
|
Осталось написать к задаче
ответ: 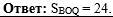
|
|
Пример 2. По данным рисунка
найдите угол FNO, если угол
MKN равен 66 градусам. |
|
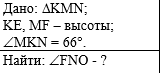 |
 |
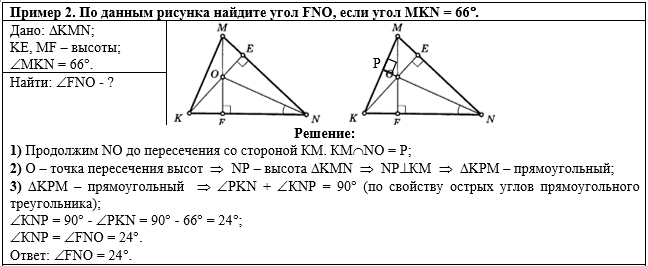
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
продолжим NO до пересечения со стороной КМ:
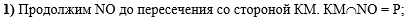
|
|
Во втором действии
зная, что О - точка пересечения высот, делаем вывод, что
NP - тоже высота треугольника
KMN, следовательно, NP
перпендикулярна КМ, тогда треугольник КРМ - прямоугольный:
 |
|
В третьем действии
зная, что треугольник КРМ - прямоугольный из суммы его острых углов
найдём угол KNP, а т.к. этот угол совпадает с
углом FNO, найдём и его:
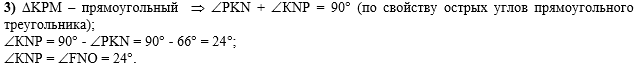 |
|
Осталось написать к задаче
ответ: 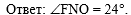
|
|
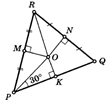
Пример 3. По данным рисунка
найдите ОК, если RO равно 20. |
|
 |
 |
Общий вид решения задачи:

|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
используем условие, что О - точка пересечения серединных
перпендикуляров, и сделаем вывод, что ОК - тоже серединный перпендикуляр
(по свойству серединных перпендикуляров к сторонам треугольника):
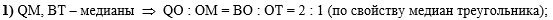
|
|
Во втором действии
из условия, что ОМ - серединный перпендикуляр к отрезку
PR, сделаем вывод, что RO =
PO = 20 (по свойству серединного перпендикуляра к отрезку):
 |
|
В третьем действии
зная, что ОК - серединный перпендикуляр к отрезку PQ,
рассмотрим прямоугольный треугольник РОК и найдём катет ОК, лежащий
против угла 30 градусов:
 |
|
Осталось написать к задаче
ответ: 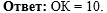
|
|
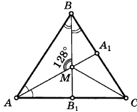
Пример 4. По данным рисунка
найдите угол МСВ1. |
|
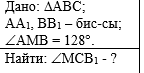 |
 |
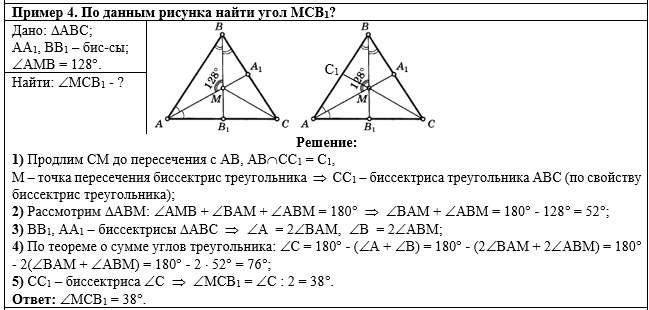
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
продлим СМ до пересечения с АВ (получим точку С1). Так как М
- точка пересечения биссектрис треугольника, то СС1 -
биссектриса треугольника АВС (по свойству биссектрис треугольника):

|
|
Во втором действии
рассмотрим треугольник АВМ и по теореме о сумме углов треугольника
найдём сумму углов ВАМ и АВМ:
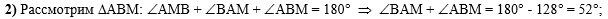 |
|
В третьем действии
из условия, что АА1 и ВВ1 - биссектрисы
треугольника АВС выразим угол А через угол ВАМ и угол В через угол АВМ:
 |
|
В четвёртом действии
по сумме углов треугольника, используя выводы, сделанные в третьем
действии найдём угол С:
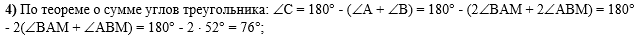
В пятом действии,
т.к. - СС1 - биссектриса треугольника АВС, найдём угол МСВ1:
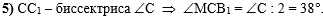
Осталось написать к задаче
ответ: 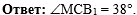
|
![]() Повторение
курса 7 класса
Повторение
курса 7 класса
![]() Четырёхугольники
Четырёхугольники
![]() Параллелограмм
и его свойства
Параллелограмм
и его свойства
![]() Трапеция
Трапеция
![]() Площади
Площади
![]() Теорема
Пифагора
Теорема
Пифагора
![]() Подобные
треугольники. Признаки подобия треугольников
Подобные
треугольники. Признаки подобия треугольников
![]() Пропорциональные
отрезки в прямоугольных треугольниках
Пропорциональные
отрезки в прямоугольных треугольниках
![]() Соотношение
между сторонами и углами прямоугольного треугольника
Соотношение
между сторонами и углами прямоугольного треугольника
![]() Окружность.
Касательная к окружности
Окружность.
Касательная к окружности
![]() Центральные
и вписанные углы
Центральные
и вписанные углы
![]() Четыре
замечательные точки треугольника
Четыре
замечательные точки треугольника
![]() Вписанная
и описанная окружности
Вписанная
и описанная окружности
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 1
ВЕРНУТЬСЯ К ПРИМЕРУ 1 ![]() ВЕРНУТЬСЯ К ПРИМЕРУ 2
ВЕРНУТЬСЯ К ПРИМЕРУ 2
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 3
ВЕРНУТЬСЯ К ПРИМЕРУ 3
![]() ВЕРНУТЬСЯ К ПРИМЕРУ 4
ВЕРНУТЬСЯ К ПРИМЕРУ 4
![]() ПЕЧАТЬ МАТЕРИАЛА
ПЕЧАТЬ МАТЕРИАЛА