Перед началом обучения обязательно
распечатайте материал для работы (нажмите на изображение ниже):
|
Обратите внимание!
В левом
столбце печатного материала находятся:
В правом
столбце печатного материала находятся:
Материал
содержит четыре разобранные задачи и пять задач предложено решить
самостоятельно.
|
 |
| Печатный
материал содержит две страницы, которые выглядят так: |
 |
|
Пример 1. Найдите гипотенузу
прямоугольного треугольника, если его катеты равны 6 и 8. |
|
 |
 |
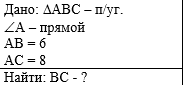Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
Так как треугольник по
условию прямоугольный воспользуемся теоремой Пифагора, найдём
сначала квадрат гипотенузы ВС, а потом саму гипотенузу:
 ,
Осталось написать ответ к
задаче:  |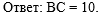
|
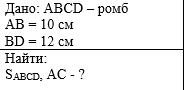
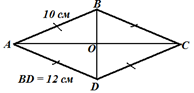
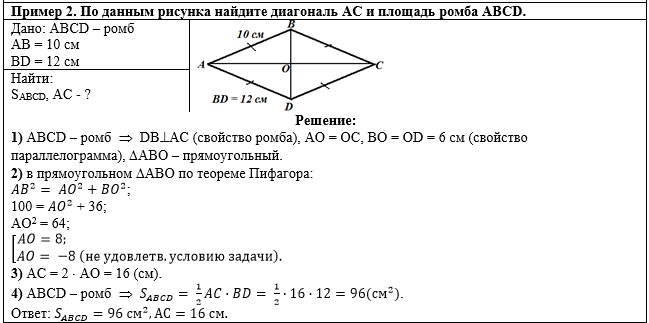
Пример 2. По данным рисунка
найдите диагональ АС и площадь ромба ABCD. |
|
 |
 |
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии из
того, что ABCD является ромбом, сделаем вывод,
что его диагонали BD и АС - перпендикулярны
(свойство ромба) и точкой пересечения делятся пополам (свойство
параллелограмма), откуда ВО = 6 см, а также сделаем вывод, что
треугольник АВО - прямоугольный:
|
|
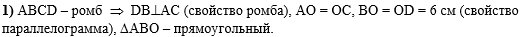
Во втором действии
рассмотрим прямоугольный треугольник АВО, в котором по теореме Пифагора
найдём неизвестный катет АО:
|
|
В третьем действии,
используя то, что О - середина АС, найдём АС:
|
|
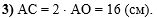
В четвёртом действии
по формуле площади ромба (площадь ромба равна половине произведения его
диагоналей) найдём площадь АВСD:
Осталось написать ответ к задаче:
|
|
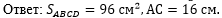
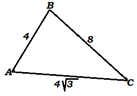
Пример 3.
В треугольнике со сторонами 4, 8 и 4√3 найдите
углы. |
|
 |
 |
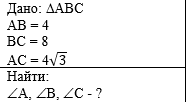Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
рассмотрим треугольник АВС. Заметив, что ВС - большая сторона, проверим,
равен ли её квадрат сумме квадратов двух других сторон:
Теперь по теореме, обратной теореме Пифагора, сделаем вывод, что
треугольник АВС - прямоугольный, в котором большая сторона является
гипотенузой и лежит против прямого угла:
|
|
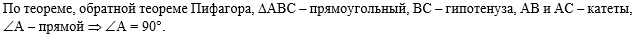
Во втором действии
по свойству прямоугольного треугольника, что катет, равный половине
гипотенузы лежит против угла, равного 30 градусам, найдём, что угол С
равен 30 градусам, так как лежит против катета АВ:
|
|
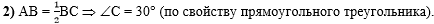
В третьем действии,
используя свойство острых углов прямоугольного треугольника, найдём угол
В:
|
|
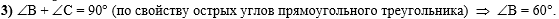
Осталось написать ответ к задаче:
|
|
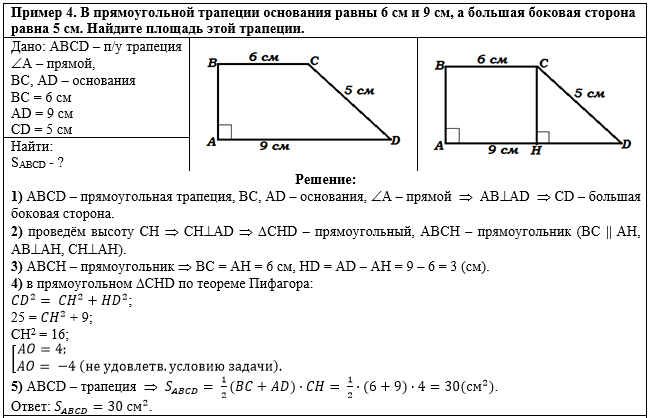
Пример 4. В
прямоугольной трапеции основания равны 6 см и 9 см, а большая боковая
сторона равна 5 см. Найдите площадь этой трапеции. |
|
 |
 |
Общий вид решения задачи:
|
|
Слева напишем краткое условие
задачи, используя условные обозначения. |
С правой стороны от краткого
условия разместим рисунок, на котором отмечены данные задачи. |
|
Под условием и рисунком
запишем слово "Решение:" |
|
В первом действии
рассмотрим прямоугольную трапецию АВСD c
основаниями ВС и AD и прямым углом А и сделаем
вывод, что большая боковая сторона трапеции - CD:
|
|
Во втором действии
проведём высоту СН и получим прямоугольный треугольник
CHD и прямоугольник АВСН:
(второй рисунок рисовать не надо - СН проводится на том
рисунке, который уже выполнен к задаче).
|
|
В третьем действии,
используя свойство противоположных сторон прямоугольника (ВС = АН),
найдем отрезок HD:
|
|
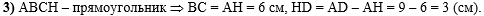
В четвёртом действии
в прямоугольном треугольнике CHD находим катет
СН по теореме Пифагора:
 |
|
В пятом действии по
формуле площади трапеции (площадь трапеции равна произведению половины
суммы оснований на высоту) найдём площадь ABCD:
 |
|
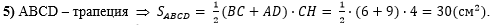Осталось написать ответ к задаче:
|
Повторение
курса 7 класса
