Раздаточный материал               Презентация  

(представлена краткая теория, рассмотрены примеры решения задач. Пример 1. Пример 2. Пример 3. Пример 4. Пример 5. Пример 6. Пример 7).

Пример 1. Пояснения к Примеру 1

1) На чертеже к задаче обязательно должны быть указаны заданные векторы;

2) Так как заданные векторы начинаются в точке А, то угол между заданными векторами имеет вершину в т. А;

3) Во втором действии по теореме косинусов находим косинус угла АВС, далее, по таблице Брадиса находим соответствующий угол. Как пользоваться таблицей Брадиса показано здесь.

Пример 2. Пояснения к Примеру 2

1) По условию треугольник АВС - равносторонний, тогда все углы треугольника равны 60 градусам. Если ВН - высота этого треугольника, то она перпендикулярна стороне, а также является медианой и биссектрисой;

2) Так как высота ВН перпендикулярна стороне АС, то угол между векторами ВН и АС - прямой, а, следовательно, косинус этого угла равен 0. Тогда и скалярное произведение этих векторов равно 0;

3) Скалярный квадрат вектора равен квадрату его длины, поэтому, чтобы найти скалярный квадрат вектора АВ, возведём его длину в квадрат.

Пример 3. Пояснения к Примеру 3

Так как заданы координаты обоих векторов, достаточно воспользоваться определением скалярного произведения векторов в координатах.

Пример 4. Пояснения к Примеру 4

Чтобы найти координату х вектора b, воспользуемся определением скалярного произведения векторов в координатах и следствием из определения (признаком перпендикулярности векторов).

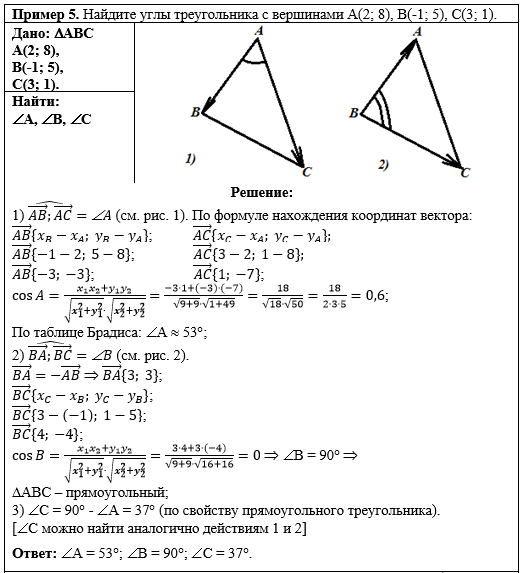
Пример 5. Пояснения к Примеру 5

1) На рисунке к задаче отмечаем векторы АВ и АС, получается, что угол между векторами равен углу А треугольника АВС.

Далее, по формуле нахождения координат вектора по координатам его начала и конца, находим координаты каждого заданного вектора.

Чтобы найти косинус угла А, воспользуемся следствием из определения скалярного произведения в координатах.

Подставив в формулу для нахождения косинуса угла найденные значения координат векторов, найдём значение косинуса угла А. Далее, по таблице Брадиса находим соответствующий угол. Как пользоваться таблицей Брадиса показано здесь.

2) Аналогично, находим угол В. Векторы АВ и ВА - противоположные векторы, следовательно, координаты вектора ВА противоположны координатам вектора АВ по знаку.

Координаты вектора ВС находим по формуле нахождения координат вектора по координатам его начала и конца.

Подставив найденные координаты векторов в формулу для нахождения косинуса угла, найдём, что косинус равен 0, а, следовательно, угол  В равен 90 градусам. Следовательно, треугольник АВС - прямоугольный.

3) Угол С можно искать аналогично углам А и В. А можно воспользоваться свойством острых углов прямоугольного треугольника.

Пример 6. Пояснения к Примеру 6

1) Так как скалярный квадрат вектора равен квадрату его длины, то длину вектора можно найти, если возвести сумму векторов в квадрат.

Так как векторы обладают теми же свойствами произведения, что и числа, можно использовать формулу сокращённого умножения (квадрат двучлена), а затем воспользоваться определением скалярного произведения.

Далее, чтобы найти длину суммы векторов, из полученного числа извлечём квадратный корень;

2) Длину разности векторов найдём аналогично, заменив "+" на "-".

Пример 7. Пояснения к Примеру 7

Раскроем заданное выражение, воспользовавшись распределительным свойством скалярного произведения векторов.

Далее, найдём каждое скалярное произведение по определению скалярного произведения векторов и сложим полученные результаты.