Основные понятия

(слева - теоретические сведения, справа - иллюстрации; добавлены задачи на построение равных векторов)

Решение задач

(разобраны две задачи на вычисление длины вектора, добавлены задачи для самостоятельного решения)

Пояснения к Примеру №1

Слева пишем "Дано" и "Найти", справа от "Дано" помещаем рисунок к задаче.

Под "Дано" и рисунком размещаем Решение задачи.

1) Так как АВСD - прямоугольник, то его противоположные стороны равны, следовательно, АВ = CD = 12 см, BC = AD = 16 см.

2) По определению длины вектора, его длина - это длина отрезка, которым он отображается. Поэтому записано:

.

3) Также по определению длины вектора: .

Диагональ BD делит прямоугольник на два прямоугольных треугольника.

Рассмотрим п/у треугольник ABD, где BD - гипотенуза. Тогда по теореме Пифагора: BD² = AB² + AD² = 144 + 256 = 400, откуда

Не забываем написать Ответ.

Общий вид решения задачи

Пояснения к Примеру №2

Слева пишем "Дано" и "Найти", справа от "Дано" помещаем рисунок к задаче.

Под "Дано" и рисунком размещаем Решение задачи.

1) Так как ВН перпендикулярен AD, то треугольник АВН - прямоугольный, сторона параллелограмма АВ в нём - гипотенуза, ВН - катет. Если по условию угол А равен 30°, то ВН лежит против угла 30°, а, следовательно, равен половине гипотенузы:

.

Длина вектора НВ равна длине отрезка ВН: .

2) Треугольник BHP также прямоугольный, ВР - гипотенуза. Если угол НВР равен 45°, то и угол ВРН также равен 45° (по свойству острых углов прямоугольного треугольника), следовательно, прямоугольный треугольник BHP является равнобедренным (по признаку равнобедренного треугольника). Тогда ВН = НР = 5 (см).

По теореме Пифагора ВР² = ВН² + НР² = 25 + 25 = 50, откуда найдём длину вектора ВР: .

Не забываем написать Ответ.

Общий вид решения задачи

Правила и законы сложения векторов

(к краткой теории - графические иллюстрации, примеры решения задач на построение равных векторов [с помощью чертёжных инструментов и на квадратной решётке])

Решение задач

(включает задачи на построение равных векторов, задачи на построение суммы векторов на квадратной решётке, задачи на применение законов сложения векторов). Разобраны две задачи на сложение векторов.

Пояснения к Примеру №1

Общий вид решения задачи:

а) векторы и - не коллинеарные. В этом случае достаточно из конца вектора построить вектор, равный вектору (голубой вектор на рисунке).

Тогда сумма этих векторов - вектор, начало которого совпадает с началом вектора , а конец - с концом вектора (красный вектор на рисунке).

б) векторы и - коллинеарные и противоположно направленные.

Также из конца вектора строим вектор, равный вектору (голубой вектор на рисунке).

Тогда сумма этих векторов - вектор, начало которого совпадает с началом вектора , а конец - с концом вектора (красный вектор на рисунке).

Задача решается одним из двух представленных способов. Оба способа использовать не нужно!

I способ: используем правило многоугольника для сложения нескольких векторов с помощью чертежа - строим заданные векторы "один за другим", совмещая начало следующего вектора с концом предыдущего. По построению конец последнего вектора совпадёт с началом первого, т.е. в данном случае сумма этих векторов - "точка М", нулевой вектор ММ.

II способ: используем переместительное и сочетательное свойства сложения векторов, а также правило треугольника: сумма двух векторов - это вектор, начало которого совпадает с началом 1 вектора, а конец - с концом 2 вектора, если начало второго вектора совпадает с концом первого.

Начало вектора НР - это конец вектора МН, поэтому сумма векторов МН и НР - это вектор МР.

Аналогично: сумма векторов МР и РО - вектор МО, далее - сумма векторов МО и ОS - вектор MS,  сумма векторов MS и SM -  равна 0, т.к. эти векторы противоположны.

Ответ:

Правила вычитания векторов

(в краткой теории - правила вычитания векторов, примеры построения разности векторов с помощью инструментов и на квадратной решётке)

Решение задач

(разобрана задача на построение суммы и разности векторов на квадратной решётке, разобрана задача на применение правил сложения и вычитания векторов).

Пояснение к примеру №1

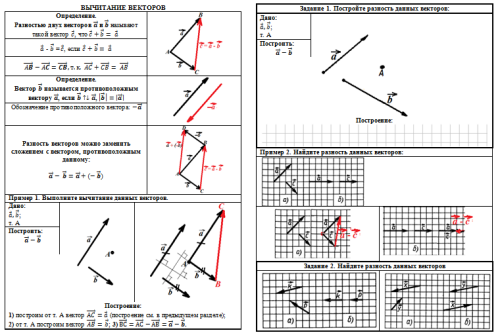Общий вид решения задачи

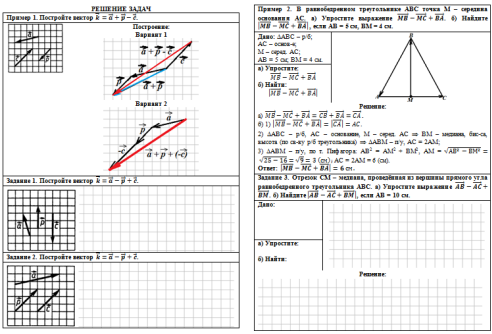
Задача решается по одному из предложенных вариантов (оба варианта использовать не нужно!).

Построение по Варианту 1: По правилу сложения векторов находим сумму векторов и . Затем пристраиваем вектор к найденной сумме и по правилу нахождения разности векторов находим разность вектора и вектора .

Построение по Варианту 2: . Поэтому необходимый результат получен по правилу многоугольника - в конец вектора пристроено начало вектора , далее в конец вектора пристроено начало вектора

а) Разность векторов МВ и МС - вектор, начало которого - конец вектора МС, конец которого - конец вектора МВ, т.е. вектор СВ. Далее, по правилу сложения векторов получаем, что сумма векторов СВ и ВА -  это вектор СА.

б) В первом действии по результату, полученному в п. а), делаем вывод, что

Во втором действии из условия, что треугольник АВС - равнобедренный, АС - его основание, а т. М - его середина, делаем вывод, что ВМ - медиана, биссектриса и высота треугольника АВС (по свойству равнобедренного треугольника), откуда получаем вывод, что треугольник АВМ - прямоугольный, а АС = 2АМ.

В третьем действии по теореме Пифагора находим катет АМ прямоугольного треугольника АВМ, а затем вычисляем длину стороны АС.

Не забываем написать ответ к задаче.