Раздаточный материал             Презентация

(представлена краткая теория, рассмотрены примеры решения задач. Пример 1. Пример 2. Пример 3. Пример 4).

Пример 1. Пояснения к Примеру 1

Так как все углы в правильном многоугольнике равны между собой, для того, чтобы найти один угол, достаточно найти сумму углов многоугольника (по формуле суммы углов) и разделить на количество сторон в многоугольнике.

Получена формула для нахождения угла в правильном многоугольнике.

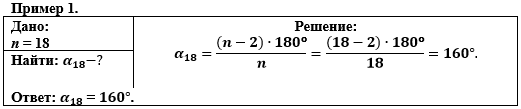Пример 2. Пояснения к Примеру 2

Воспользуемся формулой для нахождения угла в правильном многоугольнике, подставим в неё заданную величину угла и решим полученное уравнение относительно переменной n.

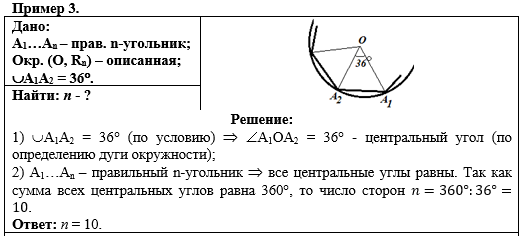
Пример 3. Пояснения к Примеру 3

В правильном многоугольнике все центральные углы между собой равны: описанная окружность делится вершинами многоугольника на равные дуги, следовательно, равны и соответствующие центральные углы.

Вся окружность соответствует углу 360 градусов, поэтому, если дуга равна 36 градусам, то и центральный угол также равен 36 градусам.

Далее, для нахождения количества сторон в правильном многоугольнике достаточно 360 градусов разделить на 36 градусов.

Пример 4. Пояснения к Примеру 4

1) Зная периметр правильного треугольника, найдём длину стороны треугольника;

2) Так как известно соотношение между длиной стороны правильного треугольника и радиусом описанной окружности, найдём радиус описанной окружности;

3) Треугольник и квадрат вписаны в одну окружность, тогда радиус окружности, описанной около треугольника, равен радиусу окружности, описанной около квадрата.

Зная соотношение между стороной квадрата и радиусом описанной окружности, подставив значение радиуса, найдём длину стороны квадрата;

4) По формуле, связывающей радиус вписанной в квадрат и описанной около квадрата окружности, найдём радиус вписанной окружности;

5) Площадь квадрата найдём, возведя сторону квадрата в квадрат (свойство площади квадрата).