Раздаточный материал     Презентация

(представлена краткая теория с выводом, разобран Пример решения треугольника).

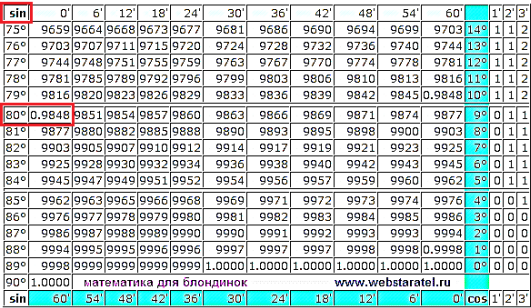
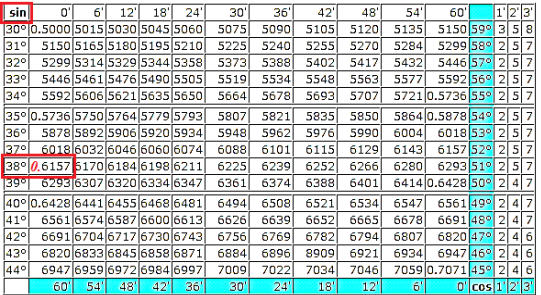
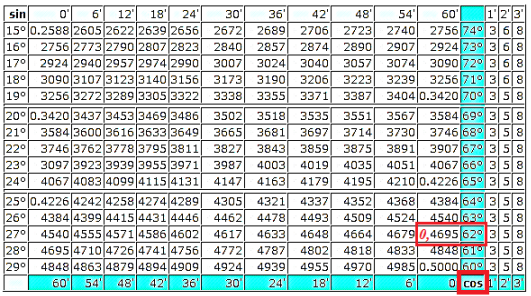
Первое действие: использована теорема синусов и найден синус угла В. Чтобы найти синус угла А (необходим для вычисления), использованы таблицы Брадиса (синус 80º примерно равен 0,98...).  Далее, по таблице Брадиса найдена примерная величина угла В - 38º.

Второе действие: по теореме о сумме углов треугольника найдена величина угла С - 62º.

Третье действие: использована теорема косинусов и найдена сторона АВ. Косинус угла 62º определён по таблице Брадиса. АВ = 14.

Четвёртое действие: использована теорема о площади треугольника. Так как синус угла В уже найден в 1 действии удобно применить в этой формуле стороны АВ и ВС. Площадь треугольника АВС равна 67,2 квадратные единицы.

Пояснения к использованию таблиц Брадиса

Так как значения синуса и косинуса по сути своей одни и те же числа, отличие только в том, что  при  изменении  угла  от  0º  до  90º  значения  косинуса угла

уменьшаются, а значения синуса угла увеличиваются. Поэтому всё, что касается синуса, в таблицах определяют по углам, представленным в крайней левой колонке (углы возрастают сверху вниз), а всё, что касается косинуса, определяют по углам, представленным в правой колонке (выделена голубым цветом, углы возрастают снизу вверх).

Первый угол, для которого ищут синус - угол А, равный 80º - см. на рисунке справа. Значение, подставленное при вычислениях, получено по правилам округления: вместо табличного 0,9848... применили 0,98... .

Получив значение синуса угла В примерно 0,6155..., находим ближайшее к нему по таблице (см. рисунок снизу) - 0,6157... . Это соответствует углу 38º (находим в левом столбце).

Для угла 62º ищем косинус (см. рисунок снизу-справа). Для этого находим угол 62º в правой колонке и выписываем значение косинуса рядом с этим углом. Это значение -  0,4695 по правилам округления примерно равно 0,5.