![]() Повторение
материала 7, 8 классов. Решение задач
Повторение
материала 7, 8 классов. Решение задач
![]() Векторы.
Сложение и вычитание векторов
Векторы.
Сложение и вычитание векторов
![]() Векторы.
Умножение вектора на число
Векторы.
Умножение вектора на число
![]() Применение
векторов к решению задач и доказательству теорем
Применение
векторов к решению задач и доказательству теорем
![]() Разложение
вектора по двум неколлинеарным векторам
Разложение
вектора по двум неколлинеарным векторам
![]() Координаты
вектора. Простейшие задачи в координатах
Координаты
вектора. Простейшие задачи в координатах
![]() Уравнение
окружности и прямой на плоскости
Уравнение
окружности и прямой на плоскости
![]() Синус,
косинус и тангенс угла. Формулы для вычисления координат точки на
плоскости
Синус,
косинус и тангенс угла. Формулы для вычисления координат точки на
плоскости
![]() Соотношение
между сторонами и углами треугольника
Соотношение
между сторонами и углами треугольника
![]() Скалярное
произведение векторов
Скалярное
произведение векторов
![]() Правильные
многоугольники
Правильные
многоугольники
![]() Длина
окружности и площадь круга
Длина
окружности и площадь круга
![]() Движения.
Основные понятия
Движения.
Основные понятия
![]() Параллельный
перенос
Параллельный
перенос
![]() Поворот
Поворот
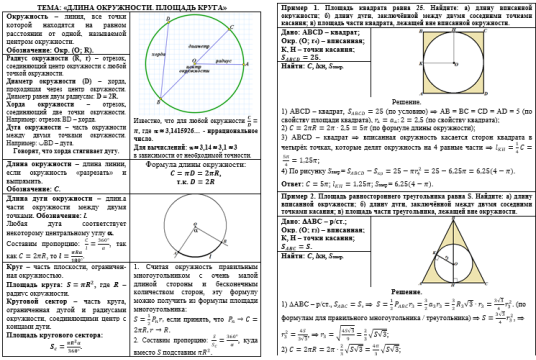
Длина окружности и площадь круга
Изучая эту тему, вы вспомните определение окружности, понятие длины окружности и площади круга;
Узнаете формулы для вычисления длины дуги окружности и площади кругового сектора;
Научитесь решать простейшие задачи по теме и более сложные, комбинированные задачи.
Раздел содержит двусторонний печатный материал с краткой теорией по теме "Длина окружности и площадь круга", разобранные примеры решения задач, а также задания для самостоятельного решения.
|
(представлена краткая теория, рассмотрены примеры решения задач. Пример 1. Пример 2. Пример 3. Пример 4. Пример 5). |
|
 |
 |
|
Пример 1. Пояснения к Примеру 1 1) Зная площадь квадрата, по свойству площади квадрата найдём сторону квадрата, как квадратный корень из значения площади. Так как радиус вписанной в квадрат окружности равен половине стороны квадрата, найдём этот радиус; 2) По формуле длины окружности найдём длину вписанной окружности; 3) Окружность, вписанная в квадрат, точками касания делится на 4 равные части, поэтому, чтобы найти длину дуги между соседними точками касания достаточно найденную длину окружности разделить на 4; 4) Площадь части квадрата, лежащей вне вписанной окружности - это разность между площадью квадрата и площадью вписанного круга. NB. Если не сказано специально, то при решении задач на длину окружности и площадь круга значение числа пи не подставляют, оставляют его обозначение как множитель. |
 |
|
Пример 2. Пояснения к Примеру 2 1) Данная задача - пример задачи, решаемой в общем виде, когда все необходимые величины выражают через заданную величину. В данном случае задана площадь правильного треугольника, следовательно, все величины надо выразить через эту площадь. Для этого воспользуемся формулами для правильных многоугольников (площади, стороны, радиуса вписанной окружности). Результат - полученное выражение для радиуса окружности, вписанной в равносторонний треугольник, через площадь этого треугольника; 2) По формуле длины окружности выразим длину вписанной окружности через заданную площадь треугольника; 3) Так как треугольник правильный, то вписанная окружность делится точками касания на три равные части. Поэтому, чтобы найти длину дуги между соседними точками касания, достаточно длину этой окружности разделить на 3; 4) Площадь части треугольника, лежащей вне окружности вычислим как разность площади треугольника и площади вписанного круга. |
  |
|
Пример 3. Пояснения к Примеру 3 1) Пользуясь формулой длины дуги, подставим в неё значение радиуса и длины окружности, найдём центральный угол, которому эта дуга соответствует; 2) В формулу площади кругового сектора подставляем заданное значение центрального угла и находим эту площадь. |
 |
|
Пример 4. Пояснения к Примеру 4 1) Подставим в формулу площади кругового сектора заданные значения площади и радиуса окружности. Найдём значение соответствующего центрального угла. 2) Хорда, длину которой надо найти, является основанием равнобедренного (т.к. две другие стороны - радиусы окружности) треугольника, лежащим против найденного центрального угла. Поэтому для нахождения длины хорды воспользуемся теоремой косинусов. Не забываем учесть, что найденный угол является тупым, а, следовательно, косинус этого угла - число отрицательное. Пояснения см. здесь. |
 |
|
Пример 5. Пояснения к Примеру 5 1) Так как заданный треугольник является прямоугольным, то длину гипотенузы АВ найдём по теореме Пифагора. Известно, что в прямоугольном треугольнике катет является средним геометрическим между гипотенузой и проекцией этого катета на гипотенузу. Проекция катета на гипотенузу получается с помощью перпендикуляра (т.е. высоты), опущенного из вершины прямого угла на гипотенузу. Отсюда найдём отрезок ВН; 2) Так как высота проведена к гипотенузе, то данный прямоугольный треугольник разделится на два прямоугольных треугольника. Высоту СН найдём по теореме Пифагора; 3) По формуле длины окружности через диаметр окружности найдём длину окружности с диаметром СН. |
 |