Раздаточный материал   

  Презентация (синус, косинус, тангенс)   Презентация (формулы для вычисления координат точки)

(представлена краткая теория, рассмотрены примеры решения задач. Пример 1. Пример 2. Пример 3. Пример 4. Задачи на построение).

Пояснения к Примеру 1

Данная задача решается с использованием основного тригонометрического тождества. Вместо квадрата косинуса подставляем числовое значение из условия, решаем простейшее квадратное уравнение.

Выбираем только положительный корень, т.к. синус угла от 0 до 180 градусов находится в пределах между 0 и 1.

Пояснения к Примеру 2

Данная задача решается с использованием основного тригонометрического тождества. Вместо квадрата синуса подставляем числовое значение из условия, решаем простейшее квадратное уравнение.

В данном случае корней будет два, т.к. косинус угла от 0 до 180 градусов находится в пределах между -1 и 1.

Пояснения к Примеру 3

В первом действии с помощью основного тригонометрического тождества находим недостающую тригонометрическую функцию с учётом того, что ищем - синус (см. Пример 1) или косинус (см. Пример 2).

Во втором действии пользуемся определением тангенса. Подставляем значение тригонометрических функций (найденное и заданное).

NB: если мы находили синус, в задаче будет только одно решение, если находили косинус, то решений будет два.

Пояснения к Примеру 4

В первом действии задаём систему координат (см. Пример 5 в теме Координаты вектора) и определяем координаты необходимых точек - у точек А и D - по заданному расположению, для точки С - используем формулы для вычисления координат точки.

Во втором действии находим координаты точки М по формулам для вычисления координат середины отрезка.

В третьем действии находим расстояние АМ по формуле расстояния между двумя точками.

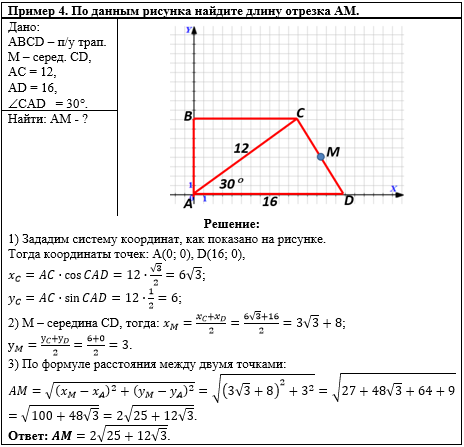Пояснения к Задачам на построение

1) Зная тангенс угла построить угол. Из курса 8 класса знаем, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Для построения угла достаточно отложить количество клеточек, равное числителю дроби, по вертикали, а количество клеточек, равное знаменателю дроби, по горизонтали.

2) Зная синус угла построить угол. Из курса 8 класса знаем, что синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. Для построения угла достаточно отложить количество клеточек, равное числителю дроби по вертикали, далее, с помощью циркуля построить точку пересечения окружности, радиус которой равен количеству клеток, соответствующему знаменателю дроби, с горизонтальной прямой.

3) Зная косинус угла построить угол. Из курса 8 класса знаем, что косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Для построения угла достаточно отложить по горизонтали количество клеток, равное числителю дроби. Далее, с помощью циркуля построить точку пересечения окружности, радиус которой равен количеству клеток, соответствующему знаменателю дроби, с вертикальной прямой.

NB. Если косинус угла выражен отрицательным числом (т.е. угол является тупым), то те же действия надо выполнить и в этом случае, только надо построить угол, смежный с полученным.